Формирование ошибок в процессе адаптивного управления (Раздел 4.2 учебника "Планово-экономическое управление"), страница 4

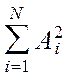
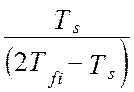
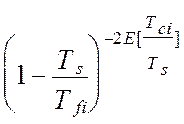                                   ´                    (4.26)             

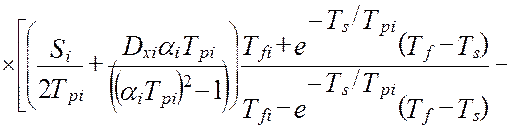
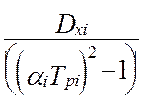
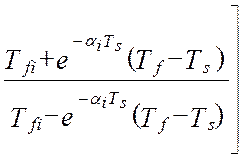
Анализ модели дисперсии выходного сигнала виртуального прибора показывает, что при стационарных входных воздействиях, X_i(t), выходной сигнал виртуального прибора является нестационарным случайным процессом. Это видно из того, что модель (4.26) является функцией реального времени.

              4.2.3. Взаимная корреляция переходных процессов

     Взаимокорреляционная функция  сигналов на выходах виртуального прибора и эталонной измерительной системы по определению [34] равна:

                    

                                                                                                                            

                     

                  

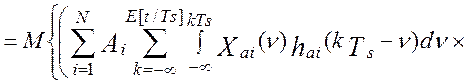
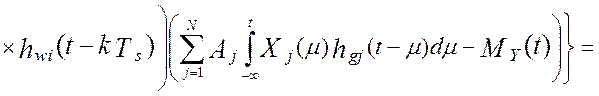
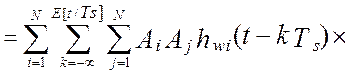
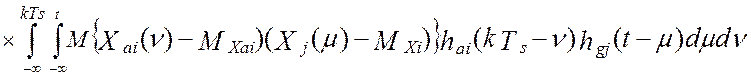
Взаимокорреляционная функция  входного сигнала i-го измерительного канала, ,  и измеряемого сигнала в j-ом канале,, по определению [34] равна: 

          Выразить корреляционную функцию  через корреляционные функции измеряемых сигналов и корреляционные функции помех, накладывающихся на полезный сигнал, можно, задавшись типом помехи и определив, например, является ли помеха коррелированной или она представляет собой белый шум. Тогда, исходное выражение  примет следующий вид [24]:

,

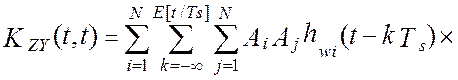
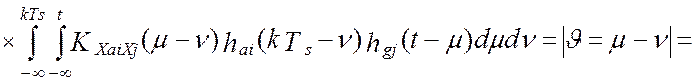
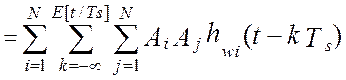
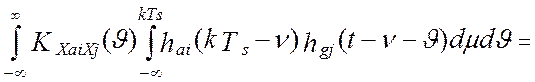
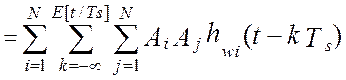
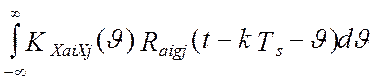где  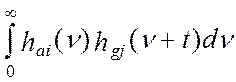есть корреляционная функция весовых функций аналоговой части i-го программно-аппаратного измерительного канала и весовой функции j-го канала эталонной измерительной системы.

          Учитывая, что взаимная корреляционная функция сигнала на выходе аналоговой части i-го канала виртуального прибора   и сигнала на выходе j-го  канала эталонной измерительной системы выражается следующим образом:

,

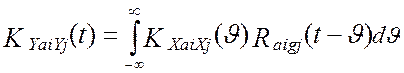то выражение для  взаимокорреляционной функции можно представить в виде [24]:

             

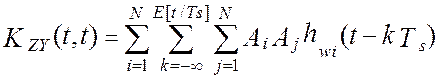
Откуда, окончательно,  модель взаимокорреляционной функции показаний эталонной измерительной системы и виртуального прибора, после подстановки типовых элементов измерительного канала, будет иметь вид [24]:

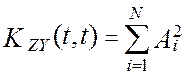
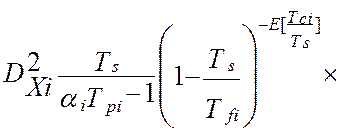                           (4.27)

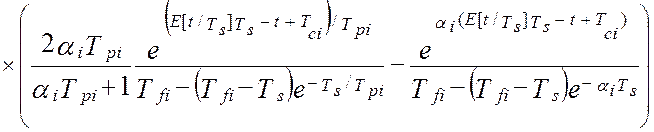
В модели (4.27),  - длина массива измерительной информации,  -коэффициенты линеаризации уравнения измерения критерия управления,  - порядковый номер измерительного канала,  - оценка дисперсии управляющего воздействия,  - скорость измеряемого сигнала,  - постоянная времени первичного преобразователя,  - постоянная времени программного динамического оператора,  - время измерения (настройка модуля ввода аналоговой информации - АЦП) и  - темп обработки информации (настройка модуля вывода аналоговой информации - регистратора - ЦАП)

           Из модели (4.27) очевидно, что взаимокорреляционная функция K_ZY(t,0) зависит от реального момента времени t, в который она была рассчитана.  Таким образом, принципиальной особенностью полученного выражения для оценки взаимокорреляционной функции показаний эталонного и виртуального приборов, , является его зависимость от текущего момента времени t, чего не наблюдалось в выражениях для оценки дисперсии показаний виртуального прибора, D²_Z  и оценки дисперсии показаний эталонной измерительной системы, D²_Y. Необходимо отметить, что в качестве аргумента взаимокорреляционной функции, , правильнее  использовать не текущее время, а величину  t=t-E[t/T_s]T_s . Эта величина не обращается в ноль вследствие не кратности (в общем случае) текущего значения реального времени, t , величине темпа обработки измерительной информации в информационно-измерительной подсистеме робастной системы, T_S.