Сигнал на выходе цифровой
части канала будет равен свертке сигнала 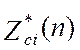 с весовой функцией цифровой части
канала:
с весовой функцией цифровой части
канала: 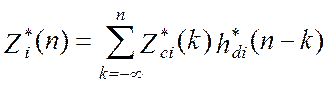 . Последним этапом преобразования
сигнала в программно-аппаратном измерительном канале является его восстановление
из цифровой формы в аналоговую:
. Последним этапом преобразования
сигнала в программно-аппаратном измерительном канале является его восстановление
из цифровой формы в аналоговую: 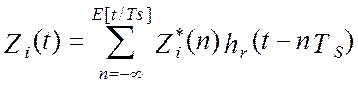 ,
,
где E[t/TS] – операция взятия целой части значения. Объединение
двух последних выражений позволяет определить модель выходного сигнала
программно-аппаратного измерительного канала, 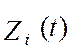 , как [24]:
, как [24]:
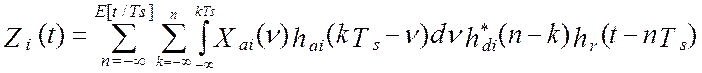 (4.23)
(4.23)
Для информационно-измерительного канала виртуального
прибора выражение представляет собой результат измерения некоторого
технологического параметра. Поэтому результат измерения в каждом из каналов 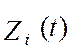 должен быть пропущен через звено с
импульсной весовой функцией [24], дополнительно появляющегося в результате
линеаризации измерительной системы. Таким образом, суммированию будут
подвергнуты не измеренные каналом сигналы
должен быть пропущен через звено с
импульсной весовой функцией [24], дополнительно появляющегося в результате
линеаризации измерительной системы. Таким образом, суммированию будут
подвергнуты не измеренные каналом сигналы 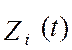 , а
сигналы
, а
сигналы 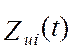 , которые равны:
, которые равны: 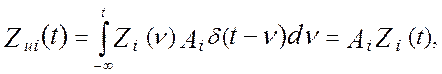 где
Аi
–коэффициенты линеаризации. Анализ схемы обработки информации в виртуальном
приборе (см. [24]) позволяет записать выходной сигнал виртуального прибора в
виде:
где
Аi
–коэффициенты линеаризации. Анализ схемы обработки информации в виртуальном
приборе (см. [24]) позволяет записать выходной сигнал виртуального прибора в
виде:
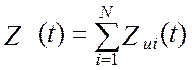 .
.
Таким образом, показания программно-аппаратной измерительной системы (виртуального прибора) можно представить следующим образом [24]:
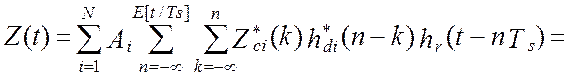
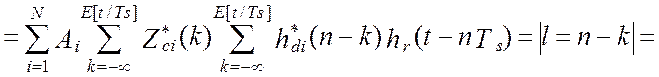
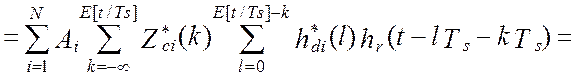
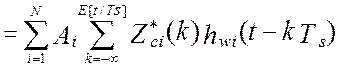
где: 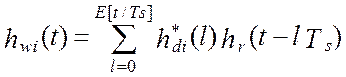 - есть
эквивалентная весовая функция цифровой части i-го канала и восстанавливающего элемента, подстановка
которого в Z(t) дает окончательное выражение для модели показаний
программно-аппаратной измерительной системы (виртуального прибора) [24, 58, 64]:
- есть
эквивалентная весовая функция цифровой части i-го канала и восстанавливающего элемента, подстановка
которого в Z(t) дает окончательное выражение для модели показаний
программно-аппаратной измерительной системы (виртуального прибора) [24, 58, 64]:
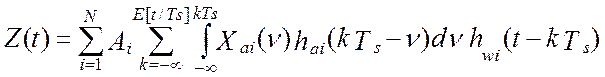 . (4.24)
. (4.24)
Математическое ожидание функции Z(t) по определению [34] равно:
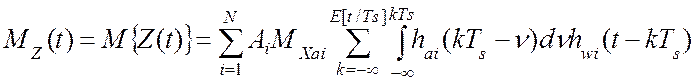
Подстановка типовых моделей элементов измерительного канала позволяет математическое ожидание показаний виртуального прибора записать как:
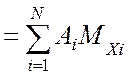
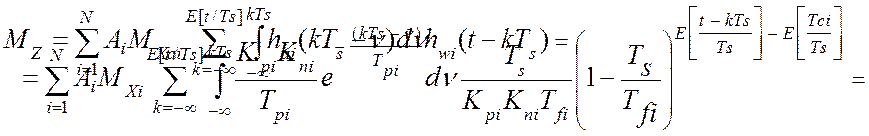 |
. (4.25)
Дисперсия показаний виртуального прибора по определению [34] равна:
![]()
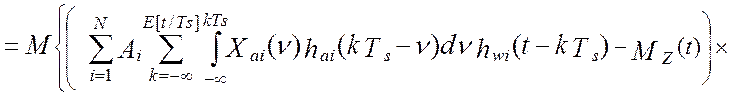
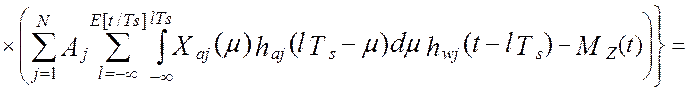
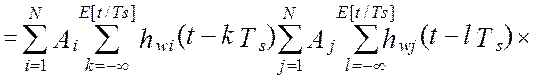
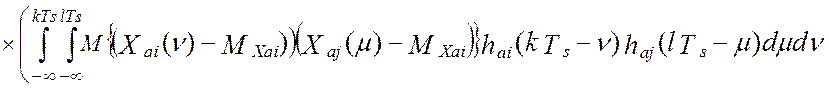
Если ввести обозначение корреляционной функции сигналов на входе аналоговой части i-го и j-го каналов как:
![]() ,
,
то выражение для дисперсии выходного сигнала виртуального прибора перепишется следующим образом:
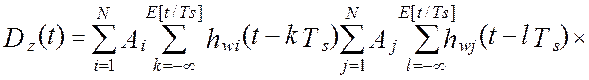
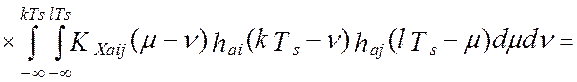
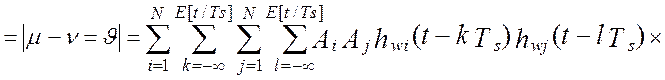
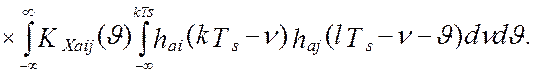
Введя замену переменных, ![]() , модель дисперсии выходного сигнала
виртуального прибора примет вид:
, модель дисперсии выходного сигнала
виртуального прибора примет вид:
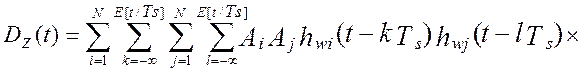
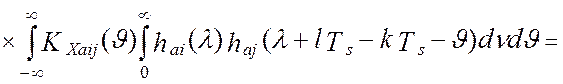
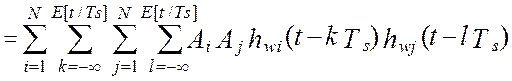
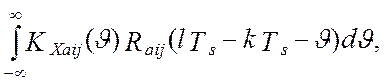
где
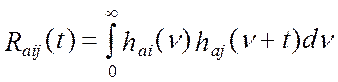
корреляционная функция весовых
функций аналоговых частей i-го и
j-го каналов. Функция ![]() позволяет выразить корреляционную функцию
сигналов на выходах аналоговой части i-го и j-го каналов по известной
корреляционной функции сигналов на входах аналоговой части i-го и j-го каналов:
позволяет выразить корреляционную функцию
сигналов на выходах аналоговой части i-го и j-го каналов по известной
корреляционной функции сигналов на входах аналоговой части i-го и j-го каналов:
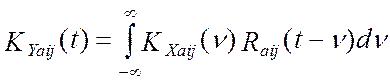
Учитывая это выражение и произведя замену переменных, m=l-k, модель дисперсии выходного сигнала виртуального прибора примет вид:
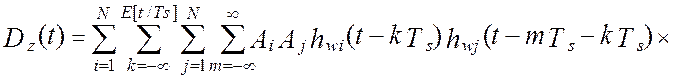
![]()
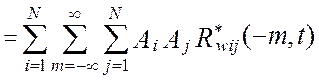
![]() ,
,
где
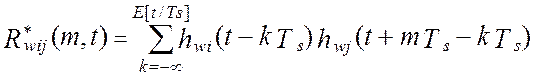
есть корреляционная
функция эквивалентных весовых функций hwn(t) i-го и j-го каналов. Функция 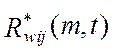 является
функцией двух аргументов, то есть для ее расчета недостаточно знать номер
отсчета m. Необходимо также знать текущее
время t. Это связано с тем, что время t в модели , в общем случае, не
кратно периоду дискретизации Ts, а, следовательно, и аргументы весовых функций hwn(t) не
укладываются в целое число отсчетов периода опроса датчиков и не могут быть
определены выражением вида nTs, где n- некоторое целое число. Таким образом, второй аргумент
функции
является
функцией двух аргументов, то есть для ее расчета недостаточно знать номер
отсчета m. Необходимо также знать текущее
время t. Это связано с тем, что время t в модели , в общем случае, не
кратно периоду дискретизации Ts, а, следовательно, и аргументы весовых функций hwn(t) не
укладываются в целое число отсчетов периода опроса датчиков и не могут быть
определены выражением вида nTs, где n- некоторое целое число. Таким образом, второй аргумент
функции 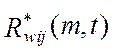 позволяет учесть значения весовых функций hwi(t) и hwj(t) в моменты
времени, которые определяются выражением tk=t-kTs (очевидно, не кратные Ts), причем превышение каждого из этих
моментов времени над k-ым
отсчетом составляет t=t-E[t/Ts]Ts. Окончательно выражение для
дисперсии выходного сигнала виртуального прибора примет следующий вид [9? 58, 64]:
позволяет учесть значения весовых функций hwi(t) и hwj(t) в моменты
времени, которые определяются выражением tk=t-kTs (очевидно, не кратные Ts), причем превышение каждого из этих
моментов времени над k-ым
отсчетом составляет t=t-E[t/Ts]Ts. Окончательно выражение для
дисперсии выходного сигнала виртуального прибора примет следующий вид [9? 58, 64]:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.