Формирование ошибок в процессе адаптивного управления (Раздел 4.2 учебника "Планово-экономическое управление"), страница 2

            Значения этой метрологической характеристики  позволяет  количественно оценить качество процесса измерения виртуальным прибором по отношению к эталонной измерительной системы. Анализ модели (4.19) показывает, что выходной сигнал виртуального прибора, даже при воздействии на нее стационарных случайных процессов, является нестационарным по корреляционной функции. А значение математического ожидания и корреляционной функции на выходе виртуального прибора зависит от времени t =T_s -T_с, характеризующего  несовпадение текущего момента времени измерения в АЦП с текущими моментами дискретизации случайного процесса. Выразим сигнал на выходе эталонной измерительной системы Y(t) как функцию от входных сигналов X₁(t), X₂(t), ..., X_N(t). Сигнал на выходе каждого из каналов, входящих в состав эталонной измерительной системы, равен: 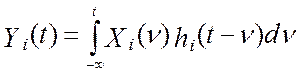,  где h_i(t) – весовая функция i-го эталонного канала. В том случае, когда канал состоит из нескольких последовательно соединенных звеньев, его весовая функция равна свертке весовых функций составляющих его звеньев. Учитывая (см. рис 4.5 и [64]), что сигнал на выходе эталонной измерительной системы, Y(t), есть сумма сверток измерительных сигналов с динамическими эталонными преобразованиями в каждом канале: 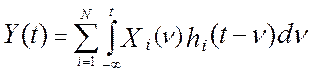 , математическое ожидание случайной функции Y(t) по определению [34] равно:

               

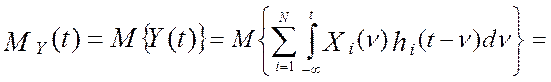
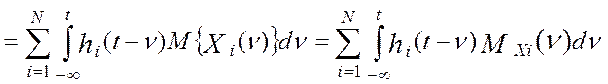                         (4.20)

Дисперсия случайной функции Y(t) по определению [34] равна :

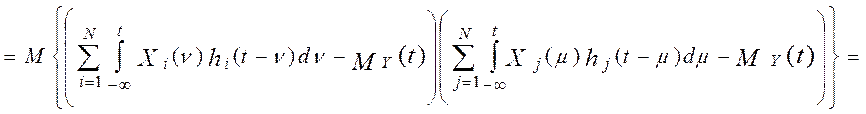
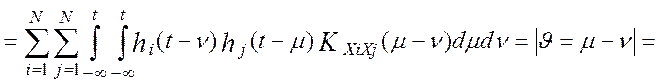
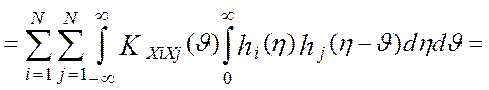
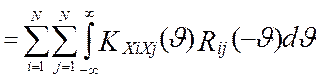                         ,                                     (4.21)

где

                                

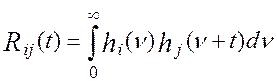
корреляционная функция весовых функций i-го и j-го измерительных каналов, а K_XiXj(t)- взаимокорреляционная функция измеряемого сигнала по разным каналам обработки информации.  Анализ модели (4.21) показывает, что дисперсия выходного сигнала эталонной измерительной системы, D_Y(t) , не зависит от реального времени. Следовательно, при стационарных входных воздействиях на измерительную систему, X_i(t), выходной сигнал эталонной измерительной системы, Y(t), является стационарным случайным процессом.

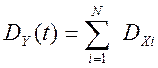                                                                                     (4.22)

        4.2.2. Вероятностные свойства показаний виртуального прибора

Вероятностные свойства переходных процессов при адаптивном управлении зависят от свойств сигнала на выходе виртуального прибора, Z(t),, который так же равен сумме сигналов от N измерительных каналов.

Согласно схеме (см. рис. 4.5), каждый программно-аппаратный измерительный канал включает в себя аналоговую часть, характеризующуюся эквивалентной весовой функцией h_ai(t), блок дискретизации измеряемого сигнала и цифровую часть, весовую функцию которой обозначим , а также восстанавливающий  элемент, преобразующий сигнал из цифровой формы в аналоговую, весовую функцию которого обозначим h_r(t).  В отличие от эталонной измерительной системы, на вход виртуального прибора поступают сигналы, X_i(t), искаженные  аддитивно наложенной помехой, G_ai(t)= X_i(t)+П_i(t). Рассмотрим основные преобразования, которым последовательно подвергается в измерительном канале виртуального прибора измеряемый сигнал. Аналоговая часть преобразует входной сигнал X_ai(t) в сигнал Z_ai(t), который равен: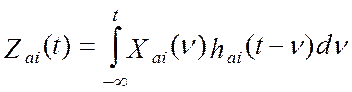                                    

В результате аналого-цифрового преобразования получаем дискретный сигнал:  , где T_S – темп обработки информации в виртуальном приборе.           Операция аналого-цифрового преобразования предполагает выполнение над сигналом двух операций: квантования по уровню и дискретизации по времени [12]:  , где E_q(t)- ошибка квантования по уровню, Т_с – время измерения величины (период квантования по уровню).