2.2.2 Паровое сопротивление конденсатора.
Паровое сопротивление конденсатора зависит от конструкции пучка трубок конденсатора, скорости паровоздушной смеси в межтрубном пространстве и удельной паровой нагрузки dк.
Паровое сопротивление современных регенеративных конденсаторов определяется по приближённой формуле ВТИ:
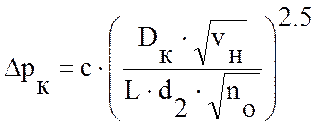 , (2.17)
, (2.17)
где с=1.8×10-4 – коэффициент, зависящий от конструкции
трубного пучка;
Dк=91.94 кг/с – количество пара, поступающего в конденсатор;
vн=29.303 м3/кг –удельный объём сухого насыщенного пара при
давлении в конденсаторе;
no=11970 шт –число охлаждающих трубок в конденсаторе.
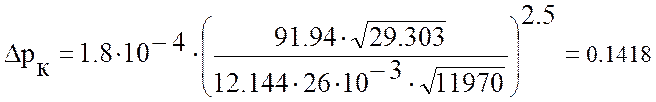 м.вд.ст.
м.вд.ст.
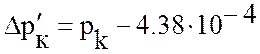 , (2.18)
, (2.18)
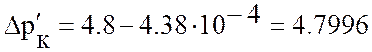 кПа.
кПа.
2.3 Прочностной расчет
Постановка задачи.
Требуется рассчитать диск конической формы по следующим данным:
n=3300-число оборотов диска в минуту;
![]()
![]() =-490 (н/см
=-490 (н/см![]() ) - радиальное
напряжение от натяга
) - радиальное
напряжение от натяга
диска при посадке;
![]()
![]() =6370 (н/см
=6370 (н/см![]() ) - радиальное
напряжение от центробежной силы лопаток и обода диска;
) - радиальное
напряжение от центробежной силы лопаток и обода диска;
у![]() =0.05 (м) – толщина
диска у основания;
=0.05 (м) – толщина
диска у основания;
у =0.012 (м) - толщина диска на периферии;
![]()
![]() (м)
– толщина кольца диска;
(м)
– толщина кольца диска;
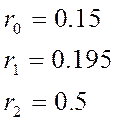 (м) – кольцевой, корневой, периферийный радиус диска.
(м) – кольцевой, корневой, периферийный радиус диска.
Вычисляем вспомогательные величины, необходимые для расчета:
а) радиус полного конуса:
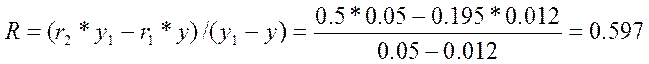 (м) , (2.19)
(м) , (2.19)
б) напряжение в тонком вращающемся кольце на радиусе R
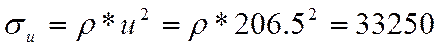 (н/см
(н/см![]() ),
(2.20)
),
(2.20)
при ![]() кг/м
кг/м![]()
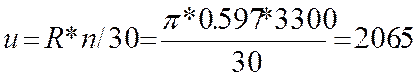 (м/с),
(2.21)
(м/с),
(2.21)
в) напряжение в тонком вращающемся кольце на
радиусе ![]() :
:
![]()
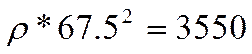 (н/см
(н/см![]() )
(2.22)
)
(2.22)
при
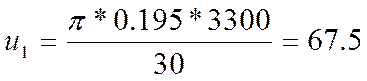 (м/с)
(2.23)
(м/с)
(2.23)
Выпишем основные формулы для определения напряжений в характерных сечениях диска.
Для конической части:
а) в сечение на радиусе ![]() :
:
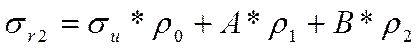 ,
(2.24)
,
(2.24)
б) в сечение на радиусе ![]() :
:
![]() ,
(2.25)
,
(2.25)
![]() ,
(2.26)
,
(2.26)
Для ступицы диска:
а) в сечение на радиусе 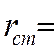
![]() :
:![]()
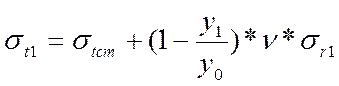 ,
(2.27)
,
(2.27)
б) на поверхность расточки диска (радиус ![]() ):
):
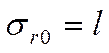
![]()
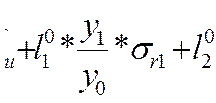 *
*![]() , (2.28)
, (2.28)
![]()
![]()
Коэффициенты ![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]()
![]()
![]() ,
, ![]()
![]() ,
, ![]()
![]() находим
по кривым (рисунок15-16) [5, с.228]
находим
по кривым (рисунок15-16) [5, с.228]
Для уравнения (6) коэффициенты находим для значения:
![]() =
=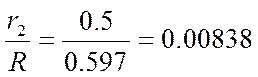 (по рисунку15-16),
(по рисунку15-16),![]()
![]() (2.29)
(2.29)
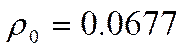 ;
; 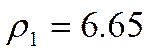 ;
; 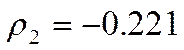 ,
,
Для удалений (2.25) и (2.26):
![]() =
=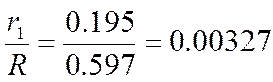 ,
(2.30)
,
(2.30)
![]()
![]() ;
;
![]() ;
; ![]() ;
;
![]()
![]() ;
; ![]()
![]() ;
; ![]()
![]() ,
,
Коэффициенты ![]()
![]() ,
, ![]() и
и ![]() :
:
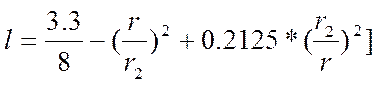 ,
(2.31)
,
(2.31)
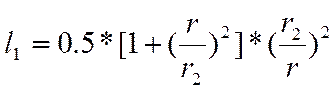 ,
(2.32)
,
(2.32) ![]()
![]()
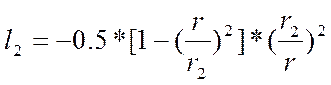 ,
(2.33)
,
(2.33)
определяем по формулам для отношений:
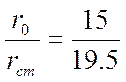 и
и
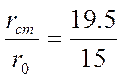 ,
(2.34)
,
(2.34)
![]()
![]() и
и ![]() .
.
Подставляя найденные коэффициенты и численные значения
вместо ![]() ,
, ![]() и
и ![]() в
уравнения (2.24), (2.25), (2.26), (2.27), (2.28) и группируя неизвестные в
левую часть уравнения, получим:
в
уравнения (2.24), (2.25), (2.26), (2.27), (2.28) и группируя неизвестные в
левую часть уравнения, получим:
![]()
![]() ,
,
![]() ,
,
![]()
![]() ,
,
![]() ,
,
-![]() ,
,
Систему этих уравнений решаем методом исключения неизвестных.
Разделив уравнение на 0.344 и сложив его с уравнением , найдем:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.