Определение эффективности стержней и запаса реактивности, страница 6

Эксперименты по уточнению эффективности компенсирующей системы и запас реактивности проводятся на критических сборках, моделирующих энергетический реактор, и на действующих энергетических реакторах. Рассмотрим вначале методы измерения запаса реактивности и эффективности компенсирующей системы на реакторе (или соответствующей критической сборке), который находится в состоянии соответствующем началу кампании. При этом реактор является критическим, а стержни КР введены в реактор. Запас реактивности в таком случае – это надкритичность реактора, если из него извлечены стержни КР. В рассмотренной ситуации достаточно измерить эффективность стержней КР, чтобы определить запас реактивности. Однако извлечь все стержни КР для измерения подкритичности невозможно, поскольку запас реактивности для реактора на быстрых нейтронах превышает β_эф и составляет, например, для реактора БН-600 примерно 6% ∆k/k_эф. Можно измерить эффективности отдельных стержней, но их сумма не будет соответствовать искомому запасу реактивности, поскольку эффективность каждого стержня в общем случае зависит от эффективности и расположения остальных.

Рассмотрим так называемый матричный метод определения эффективности системы стержней и его частный случай – метод парной интерференции [43]. Обозначим F функцию, которая описывает реактивность реактора в зависимости от количества присутствующих в нем стержней, причем извлечение одного і-го стержня в присутствии остальных N – 1 стержней приводит к увеличению реактивности на величину ρ_i. Тогда F(0,0,0,…,0) – это реактивность реактора со всеми стержнями в зоне, F(0,0,0,…, ρ_i,0) – реактивность реактора при одном извлеченном стержне и, очевидно,

ρ_i = F(0,0,0,…, ρ_i,0) - F(0,0,0,…,0).

Задача ставится следующим образом: найти значение функции F(ρ₁,ρ₂,…, ρ_N), т.е. реактивности реактора при всех извлеченных стержнях, используя значения функции F(ρ₁,0,0,…,0); F(0,ρ₂,0,…,0) и т.д.

Функцию F(ρ₁,ρ₂,…, ρ_N) можно разложить в ряд Маклорена вблизи значения F(0,0,0,…,0):

F(ρ₁,ρ₂,…, ρ_N) = F(0,0,…,0) +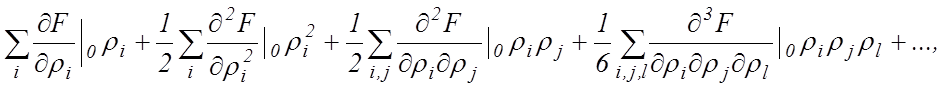

                                                                                                                    (10.1)

где

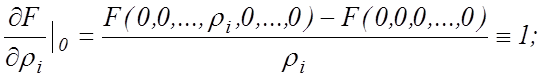
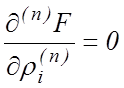            при  n >1;

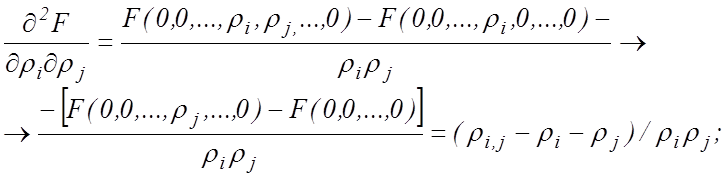
Введем обозначения

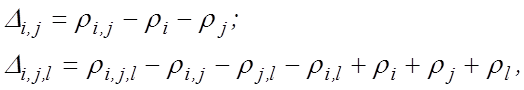                                         (10.2)

причем ρ_i,j – эффективность двух (i-го и j-го) стержней в присутствии остальных N – 2 стержней. Аналогично ρ_i,j,l – эффективность трех стержней в присутствии остальных N – 3 стержней.

Изменение реактивности реактора при извлечении всех стержней можно окончательно записать в виде

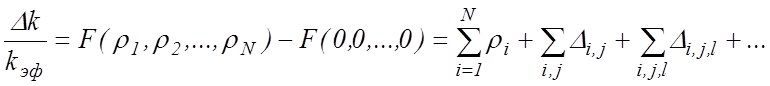             (10.3)

Рис. 10.2. Схема расположения стержней КР в реакторе БН-600

В соответствии с (10.3) в первом приближении эффективность системы стержней есть 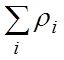, т.е. сумма эффективностей стержней, измеренных в присутствии остальных N – 1. Второе приближение требует учета парных взаимодействий стержней, т.е. величин ∆_{i, j}. В основе метода парной интерференции лежит предположение, что 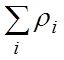 »  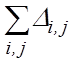» 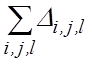. В этом случае

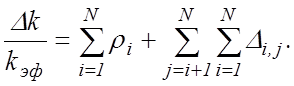                                                                          (10.4)

Обычно измеряют коэффициенты парной интерференции η _i,j, которые определяются как следующее отношение:

                                         η _i,j = ρ_i,j / ( ρ_i + ρ_j).                                            (10.5)

Комбинируя (10.2) и (10.5), находим связь между ∆_{i, j} и η _i,j:

                                        ∆_{i, j} = (η _i,j – 1)( ρ_i + ρ_j).                                       (10.6)

Принимая во внимание (10.6), эффективность системы компенсирующих стержней можно выразить через коэффициенты парной интерференции:

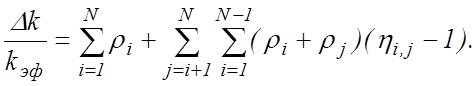                                                (10.7)

Таким образом, задача по определению эффективности системы компенсирующих стержней свелась к измерению эффективностей отдельных стержней ( в присутствии всех остальных) и коэффициентов парной интерференции.