Определение эффективности стержней и запаса реактивности, страница 10

В водо-водяных корпусных реакторах запас реактивности осуществляется с помощью подвижных компенсаторов реактивности, называемых стержнями АРК, и изменениями концентрации борной кислоты в теплоносителе. Стержни АРК представляют собой трубы из бористой стали, внутри которых проходит теплоноситель. Такие стержни называют ловушками нейтронов. В реакторе ВВЭР – 440 размещено 37 стержней АРК, а запас реактивности составляет 15 – 20% в зависимости от конкретной конструкции реактора и позволяет производить только одну остановку реактора в год для частичной перегрузки топлива.

Эффективность системы компенсирующих стержней определяют в специальных опытах на критических сборках (моделях реакторов), при физическом пуске реакторов и в процессе их эксплуатации. Это связано с тем, что точность расчетного предсказания эффективности недостаточна и требует корректировок на основе опытных данных. Кроме того, в отличие от реакторов на быстрых нейтронах эффективность компенсирующей системы критической сборки более существенно зависит от температуры, от состояния активной зоны (начальное, средне стационарное и т.д.), а также от того, какие ТВС (свежие, выгоревшие) находятся рядом со стержнями АРК, и глубины выгорания самих поглощающих элементов.

Обычно при изучении эффективности компенсирующей системы, как на критических сборках, так и в реакторах используют метод надкритической достройки, в основе которого лежит описание реактора в одно-групповом диффузионном приближении. Суть этого метода поясним на следующем примере, следуя работе [2]. Пусть в однородном цилиндрическом критическом реакторе уровень замедлителя находится при h_кр1. Ставится задача определить надкритичноть (или подкритичноть) этого реактора при других уровнях замедлителя. Особый интерес представляет случай, когда h>h_кр1, поскольку, если при новом значении k_эф ρ > β_эф, этот опыт не может быть осуществлен непосредственно. Другими словами, ставится задача определить запас реактивности в реакторе, если уровень замедлителя поднят на некоторую высоту при сохранении радиальных размеров.

В одно-групповом диффузионном приближении

                       k_эф = k_∞/(1 + В²М²),                                                         (10.11)

где В² – материальный параметр; М² – площадь миграции; k_∞ - эффективный коэффициент размножения для реактора бесконечных размеров с данной композицией.

Запас реактивности (или реактивность) реактора, в котором уровень замедлителя выше критического при данном радиусе, составит

                ρ = (k_эф – 1)/ k_эф =1 – (1 + В²М²)/ k_∞.                                     (10.12)

Найдем связь между приращениями ρ и уровня замедлителя, т.е. дρ/дh. Из (10.12) получаем, что дρ/дВ² = - М²/ k_∞, а вблизи критического состояния

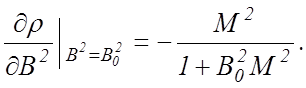                                                                      (10.13)

Для цилиндрического реактора в критическом состоянии геометрический параметр В²₀ (В² = В²₀ в критическом состоянии), как известно, можно записать в виде

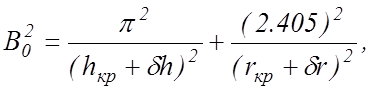                                                             (10.14)

где h_кр,r_кр – высота и радиус активной зоны критического реактора; дh и дr – экстраполированные добавки отражателя по высоте и радиусу активной зоны.

Предполагая, что переменные r и h разделяются, из (10.14) находим

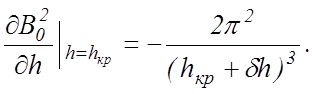                                                                     (10.15)

Предположение о разделении переменных, вообще говоря, нельзя доказать строго. Однако как показали многочисленные данные, это предложение реализуется с хорошей точностью.

Комбинируя (10.13) и (10.15), получаем

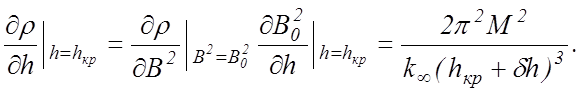                               (10.16)

Можно найти запас реактивности реактора, если уровень замедлителя поднят от  h_кр1 до h₂, интегрируя (10.16):

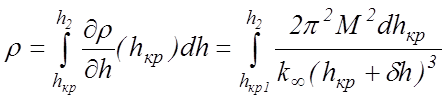                                                  (10.17)

или

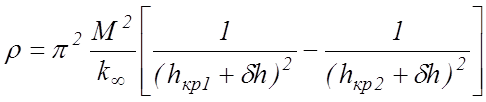                                                    (10.18)

при условии, что дh ≠ f (h_кр).

Таким образом, интегрирование дρ/дh (h_кр) в пределах от h_кр1 до h_кр2 позволяет получить запас реактивности в критическом реакторе с заданным r_кр и h_кр1, если уровень замедлителя поднять до h₂, который может быть интерпретирован как изменение В²₀, обусловленное вариацией высоты активной зоны при постоянном ее диаметре.