Лабораторная работа
Определение показателей надежности деталей и сопряжений.
Цель работы: Получение практических навыков в определении основных показателей надежности деталей и сопряжений строительных машин.
1.1.Данные для задания.
1.2. Выполнение работы.
Основными показателями надежности деталей являются дифференциальная
![]() и
интегральная
и
интегральная ![]() функции распределения наработки деталей до
первого отказа, вероятность безотказной работы
функции распределения наработки деталей до
первого отказа, вероятность безотказной работы ![]() , средняя
наработка до первого отказа
, средняя
наработка до первого отказа ![]() , интенсивность отказов
, интенсивность отказов ![]() .
.
Данные, полученные в результате обработки исходных значений интервалов
и их частот приводим в таблице 1.
Таблица 1.
![]()
1.3. Данные таблицы 1 используем для построения графиков, наглядно характеризующих эмпирическое распределение случайной величины,-
гистограммы и полигона. ( Рис. 1).
При построении гистограммы: на горизонтальной оси графика – значения,
соответствующие границам частичных интервалов, а на вертикальной оси-
частости по отдельным интервалам.
Гистограмма представляет собой ступенчатый многоугольник, а полигон –
Ломаную линию.
По гистограмме и полигону заключаем, что наиболее вероятная наработка деталей сопряжения до первого отказа находится в интервале значений от
до часов.
1.4. Числовые значения
статистических характеристик распределения случайной величины ( ![]() ,
, ![]() ,
, ![]() ) определяются по уравнениям:
) определяются по уравнениям:
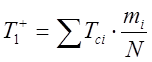
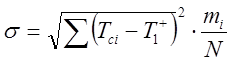
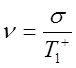
Для расчета значений ![]() и s удобнее
использовать метод сумм. ( таблица 2).
и s удобнее
использовать метод сумм. ( таблица 2).
В две первые графы таблицы 2
переписываем значения из табл.1. Затем в третьей графе делаем прочерк против
наибольшего значения частоты ![]() , а
, а
в четвертой графе – три прочерка: против прочерка в третьей графе, сверху и снизу от него; далее в третьей графе выполняем последовательное сложение
нарастающим итогом значений ![]() по частичным интервалам, начиная от
первого до прочерка и от последнего до прочерка. Полученные суммы складываем и
получаем значения двух вспомогательных коэффициентов
по частичным интервалам, начиная от
первого до прочерка и от последнего до прочерка. Полученные суммы складываем и
получаем значения двух вспомогательных коэффициентов
![]() и
и ![]() .
Аналогично получаем значения двух вспомогательных коэффициентов
.
Аналогично получаем значения двух вспомогательных коэффициентов ![]() и
и ![]() по
четвертой графе.
по
четвертой графе.
Таблица
2. Определение значений ![]() и
и ![]() методом сумм.
методом сумм.
Подсчитываем вспомогательные коэффициенты:
![]()
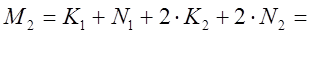
Тогда
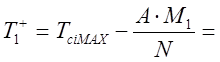
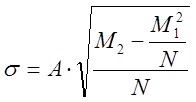
где ![]() значение
середины частичного интервала с максимальной частотой отказов, против которого
сделан прочерк в третьей графе.
значение
середины частичного интервала с максимальной частотой отказов, против которого
сделан прочерк в третьей графе.
![]() значение наработки в границах
частичного интервала ( шаг интервала)
значение наработки в границах
частичного интервала ( шаг интервала)
![]()
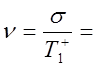
При ![]() -
нормальный закон распределения
-
нормальный закон распределения
![]() - закон распределения Вейбулла.
- закон распределения Вейбулла.
В нашем случае ![]() , что < 0,33,
следовательно, для дальнейших расчетов
, что < 0,33,
следовательно, для дальнейших расчетов
принимаем нормальный закон распределения наработки деталей сопряжения
до первого отказа.
1.5. Статистические оценки
вероятности безотказной работы ![]() и интенсивности отказов
и интенсивности отказов
![]() деталей сопряжения для
деталей сопряжения для ![]() х частичных интервалов определяются по
уравнениям:
х частичных интервалов определяются по
уравнениям:
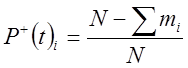
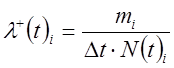
где ![]() -
число изделий в начале испытаний;
-
число изделий в начале испытаний;
![]() -
число отказавших изделий к концу i- го интервала
-
число отказавших изделий к концу i- го интервала
![]() -
значение наработки в частичном интервале ( шаг интервала)
-
значение наработки в частичном интервале ( шаг интервала)
![]() -
число работоспособных изделий к началу i-го частичного
интервала.
-
число работоспособных изделий к началу i-го частичного
интервала.
Исходные данные для расчета и их результаты приведены в таблице 3.
Таблица 3. Определение
статистических оценок ![]() и
и ![]() .
.
1.6. С использованием соответствующих значений для частичных
интервалов таблиц 1 и 3 строим графики изменения опытной вероятности
безотказной работы ![]() и эмпирической интегральной функции
и эмпирической интегральной функции
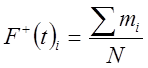
Данные графики представлены на рис. 2
Между показателями надежности
![]() и
и ![]() существует
взаимосвязь, обусловленная уравнением:
существует
взаимосвязь, обусловленная уравнением:
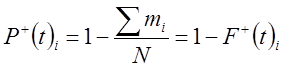
1.7. Интегральная функция
распределения ![]() может быть задана аналитически
или представлена в виде графика ( рис 2 ).
может быть задана аналитически
или представлена в виде графика ( рис 2 ).
Значения теоретической
интегральной функции ![]() для нормального распределения с
известными параметрами
для нормального распределения с
известными параметрами ![]() и
и ![]() определяются по табличному интегралу
определяются по табличному интегралу ![]() .
.
Значения функции ![]() в конце i-го частичного
интервала принимаются
в конце i-го частичного
интервала принимаются
равными значениям интеграла ![]() ( табл. прил. [2] )
( табл. прил. [2] )
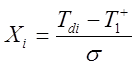
где ![]() -
верхняя граница i- го частичного интервала значений наработки деталей
до первого отказа.
-
верхняя граница i- го частичного интервала значений наработки деталей
до первого отказа.
Полученные в результате расчетов значения приведены в таблице 4.
Таблица 4. Проверка соответствия эмпирического и теоретического распределения наработки деталей сопряжения до первого отказа
по критерию l.
1.8. Проводим проверку соответствия теоретического и эмпирического
распределений по критерию согласия l академика А.Н. Колмогорова.
По таблице 4 определяем максимальное абсолютное значение разности
![]() между
эмпирической и теоретической интегральными функциями
между
эмпирической и теоретической интегральными функциями
распределения для отдельных i-х частичных интервалов.
![]()
Из табл. 4 находим ![]() .
.
Используя значение ![]() определяем число l ( критерий Колмогорова ):
определяем число l ( критерий Колмогорова ):
![]()
![]()
![]()
Для ![]() (
табл. 1 прил. 2 [1] ) находим значение вероятности
(
табл. 1 прил. 2 [1] ) находим значение вероятности ![]() ,
используя метод интерполяции:
,
используя метод интерполяции:
Таким
образом, ![]()
Поскольку вероятность ![]() больше принятого уровня значимости
больше принятого уровня значимости
![]() , то
принятая гипотеза о применимости закона нормального распределения к
эмпирическому распределению наработки деталей сопряжения до первого отказа не
отвергается. Поэтому можно говорить
, то
принятая гипотеза о применимости закона нормального распределения к
эмпирическому распределению наработки деталей сопряжения до первого отказа не
отвергается. Поэтому можно говорить
о соответствии теоретического и эмпирического распределений, а расхождение между экспериментальными и теоретическими данными
( ![]() ) можно
считать случайными.
) можно
считать случайными.
1.9. Интервальная оценка средней наработки деталей сопряжения
до первого отказа в отличие от оценки путем подсчета среднего арифметического значения позволяет получить результат с наперед
заданной достоверностью, или доверительной вероятностью ![]() .
.
Нижняя ![]() и верхняя
и верхняя ![]() границы доверительного интервала для
средней наработки
границы доверительного интервала для
средней наработки ![]() определяются по уравнениям:
определяются по уравнениям:
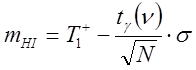
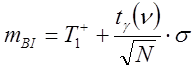
где ![]() квантиль распределения t ( Стьюдента ) с
квантиль распределения t ( Стьюдента ) с ![]() степенями
степенями
свободы для статистической выборки из ![]() значений. ( табл. 2 прил. 2 [1] ).
значений. ( табл. 2 прил. 2 [1] ).
Для ![]() и
и ![]()
![]()
Чтобы его вычислить, используем метод двойного интерполирования:
Полученные данные подставляем в выражение и находим его значение:
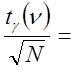
Исходя из этого определяем
![]()
![]()
Вывод: с вероятностью ![]() можно утверждать, что значение средней
можно утверждать, что значение средней
наработки деталей сопряжения до первого отказа находится в интервале
от до часов.
Литература.
1.Оценка показателей надежности элементов строительных машин. Метод. указания к лаб. раб./ Сост. Е.В. Павлов, А.Ф. Крюков.- Волгоград : ВолгИСИ, 1989.
2. Волков Д.П., Николаев С.Н. Надежность строительных машин и обору-
дования. М. Высш. шк., 1979.
3. Гриневич Г.П., Алферов А.К. и др. Надежность строительных машин.
М., Стройиздат, 1975.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.