Определение коэффициента трения качения и логарифмического декремента затухания колебаний с использованием наклонного маятника

1.  Цель работы: Определение коэффициента трения качения и логарифмического декремента затухания колебаний с использованием наклонного маятника и сменных образцов из различных материалов, устанавливаемых под разными углами наклона.

2.       Теоретические основы работы

На любое движущееся тело действуют силы трения, возникающие в результате сопротивления движению со стороны окружающей среды и других тел, с которыми оно соприкасается во время движения. В результате действия сил трения происходит превращение механической энергии во внутреннюю энергию трущихся тел, т.е. в энергию теплового движения их частиц.

Природа сил трения может быть различна.

Внутреннее трение (вязкость) состоит в возникновении касательных сил, препятствующих перемещению частей одного и того же тела по отношению друг к другу, например, в жидкостях и газах.

Внешнее трение заключается в возникновении в месте контакта двух соприкасающихся тел касательных сил, которые препятствуют относительному перемещению этих тел. Это трение обусловлено шероховатостью соприкасающихся поверхностей; в случае очень гладких поверхностей трение обусловлено силами межмолекулярного притяжения.

Если соприкасающиеся тела неподвижны друг относительно друга, имеет место трение покоя, если происходит относительное перемещение этих тел, то в зависимости от характера их относительного движения различают трение скольжения, качения и верчения.

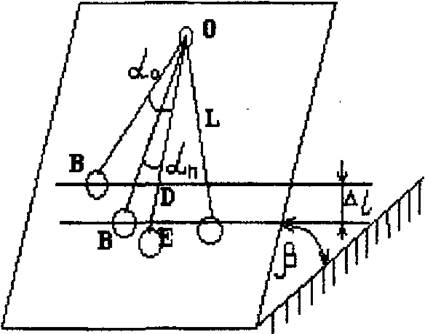
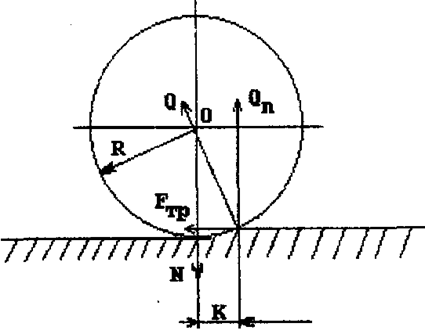
Рассмотрим трение качения, которое возникает при перекатывании шара по плоской поверхности (рис. 2.1).

При качении шара по плоской поверхности возникают деформации. Поэтому точка приложения силы Q  реакции поверхности не совпадает с линией действия силы нормального давления N. в нашем случае равной весу шара. Нормальная

составляющая Q_n этой реакции к плоскости практически равна приложенной нормальной нагрузке N, а горизонтальная составляющая представляет собой силу трения F_тр. Отсюда:

F_тр*R = Q_nK,   (2.1)

где К - плечо силы; R - радиус шара.

Или

F_тр = KN/R   (2.2)

Величину К называют коэффициентом трения качения.

Рис. 2.2

Рис. 2.1

При перекатывании наклонного маятника по плоской поверхности сила трения вызывает затухание колебаний маятника, так как потенциальная энергия, сообщенная ему при отклонении от положения равновесия, постепенно расходуется на работу по преодолению этой силы ΔW = A_тр.

Или

mgΔl*sinb = Kmgcosb*S/R   (2.3)

где:

m - масса маятника,

Δl - изменение высоты подъема шара в результате действия силы трения,

S - путь, пройденный шаром за n полных колебаний,

b - угол наклона маятника.

Из последнего выражения, учитывая геометрические соотношения для S и Δl, (рис.2.2) получим:

K = Rtgb*(cosa_n - cosa₀)/2n(a₀ - a_n) = Rtgb(a₀ + a_n)/4n   (2.4)

где n - число полных колебаний,

a₀ - угол начального отклонения в радианах,

a_n - угол, считанный после n полных колебаний в радианах.

Так как амплитуда с каждым колебанием уменьшается, то данные колебания являются затухающими.

Свободные затухающие колебания в общем случае описываются дифференциальным уравнением:

D²S/dt² + 2d*dS/dt + w₀²S = 0,   (2.5)

где S - колеблющаяся величина, описывающая физический процесс;

d - коэффициент затухания,

w₀ - циклическая частота свободных незатухающих колебаний той же системы. В случае малых затуханий решение уравнения (2.5)   имеет вид:

S = A₀*e^-dT*cos(wt + j)   (2.6)

Где A₀*e^-dT - амплитуда затухающих колебаний,

А₀ - начальная амплитуда.

Величина w = Öw₀² - d²  называется   циклической   частотой   затухающих колебаний,  промежуток  времени  между  двумя   последующими  максимумами колеблющейся величины - периодом затухающих колебаний.

T = 2p/w = 2p/Öw₀² - d²   (2.7)

Если А(t) и А(t + Т) - амплитуды двух последовательных колебаний, соответствующих моментам времени, отличающимся на период, то отношение

A(t)/A(t + T) = e^dT

называется  декрементом   затухания,   а   его   логарифмическим   декрементом затухания является

q = ln(A(t)/A(t + T)) = dT   (2.8)

Логарифмический декремент затухания - постоянная для данной колебательной системы величина.

В нашей работе амплитудой является максимальное отклонение шара от положения равновесия:

a₀ – начальная амплитуда;

a_n - амплитуда после n полных колебаний.

Поэтому формула (2. 8) примет вид:

q = 1/n*ln(a₀/a_n)   (2.9)

3. Описание установки

Общий вид установки изображен на рис.3.1. На вертикальной стойке 2 основания 1 размещен червячный редуктор, который осуществляет поворот и фиксацию нижнего кронштейна 3. Червячный редуктор приводится во вращение маховиком. Отсчет угла наклона образца производится по шкале 4.