Определение константы равновесия гомогенной реакции от температуры

Цель работы:

1.  Определение константы равновесия гомогенной реакции от температуры.

2.  Ознакомление с расчетом термодинамических функций по константе химического равновесия.

Теоретическая часть.

Зависимость константы химического равновесия от температуры выводится, во-первых, из уравнения нормального химического сродства - изотермы Вант - Гоффа:

DG^° = A _p = RT In K _p                                                                                                            (2.1)

и, во - вторых, из уравненияГиббса - Гельмголбца:

DG^°_T  = DH^°_T - TDS^°;                                                                     (2.2)

DG^°_T  = DH^°_T +T * (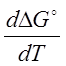)                                                               (2.3)

удобно сочетающих первый и второй законы термодинамики применительно к обратимым изотермическим процессам, где

 DH^°_T - стандартный тепловой эффект реакции;

DS^°- стандартное изменение энтропии.

Для нахождения зависимости константы химического равновесия от температуры возьмем производную по температуре от уравнения изотермы (2.1):

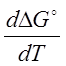- ()_р = RinK_p + RT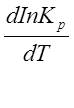                                                        (2.4)

Подставив значения DG ( 2.1) и ее производной по температуре (2.4) в уравнение ( 2.3), получим:

- RTInK_p = DH^° - RTInK_p – RT²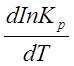                                           (2.5)

или после преобразования:

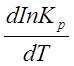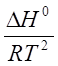 =                                                                                (2.6)

где 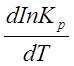  - температурный коэффициент константы химического равновесия.

Выражение (2.6.) называется уравнением изобары Вант - Гоффа. Если процесс протекает в постоянном объеме, то зависимость константы равновесия от температуры определяется уравнением изохоры Вант - Гоффа, которое выводится аналогично:

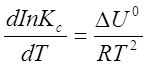                                                                                 (2.7)

где DU - стандартное изменение внутренней энергии системы.

Для реакций, протекающих в неидеальных растворах, в уравнении изохоры К_сзаменяется на К_а (с - концентрация заменяется активностью а):

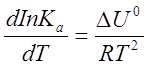                                                                                (2.8)

Уравнения (2.6), (2.7) и (2.8) показывают, если реакция протекает с выделением тепла DH < 0, DU < 0), то

.

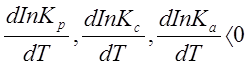Следовательно,  с  повышением  температуры  константа  равновесия уменьшается и равновесие смещается в сторону обратной реакции. Поэтому экзотермические реакции необходимо проводить при пониженной, а эндотермические - при повышенной температуре.

Уравнения изобары (2.6) и изохоры (2.7 и 2.8) определяют зависимость констант равновесия от температуры в дифференциальном виде. Для практических расчетов характеристик равновесий следует проинтегрировать эти уравнения в пределах двух температур с учетом, что тепловой эффект реакции DH в небольшом температурном интервале изменяется незначительно и его можно считать постоянным. При таком допуске интегрирование уравнения (2.6) приводит к выражению:

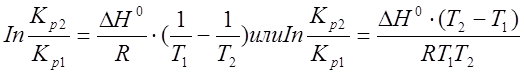                                  (2.9)

Это уравнение позволяет,

во - первых, вычислить стандартный тепловой эффект реакции  DH⁰ по экспериментально найденным при двух температурах константам равновесия; во - вторых, вычислить константу равновесия при заданной температуре, если известный стандартный тепловой эффект реакции и константа равновесия при другой температуре.

Точное значение теплового эффекта реакции, учитывающее его зависимость от температуры Т, рассчитывается по закону Кирхгофа:

DH⁰_г = DH⁰₂₉₈ + 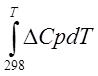                                                      (2.10)

где DH⁰₂₉₈ определяют по стандартным теплотам образования;

DС_р - изменение теплоемкости веществ в процессе реакции.

Неопределенный интеграл уравнения изобары Вант - Гоффа (2.6) дает:

InK_p = - 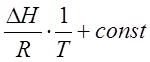                                                                    (2.11)

При переходе к десятичному логарифму получим

IgK_p= - 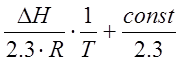                                                        (2.12)

Обозначим постоянные .слагаемые буквами А и В, тогда уравнение (2.12) примет вид

IgK_p = 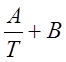                                                                                  (2.13)

Выражения (2.12) и (2.13) удобны для графического анализа процессов, так как зависимость в координатах lgK_p=f(1/T) представляет собой прямую линию, где

А=- 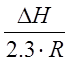 - угловой коэффициент прямой;

B = 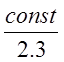отрезок абсциссы, отсекаемой этой прямой и равный IgK_p при 1/T= 0.

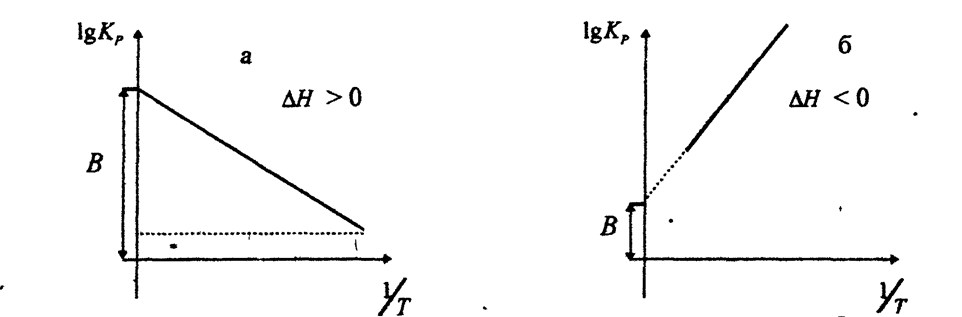
Рис.1. Зависимость логарифма константы равновесия от величины обратной температуры.