Задача параметрической оптимизации при проектировании емкости заданного объема при минимальной стоимости и максимального объема при заданной стоимости

Вариант №1

1.  ЗАДАЧА ПАРАМЕТРИЧЕСКОЙ ОПТИМИЗАЦИИ ПРИ ПРОЕКТИРОВАНИИ ЕМКОСТИ ЗАДАННОГО ОБЪМА ПРИ МИНИМАЛЬНОЙ СТОИМОСТИ

1.1.  ЦЕЛЬ РАБОТЫ:

Научиться делать постановку простых задач параметрического синтеза на примере проектирования емкости заданной структуры, освоить использование программной системы TurboC, уметь написать и отладить программу на языке С⁺⁺ и получить конкретные результаты на ПК.

1.2.  ЗАДАНИЕ:

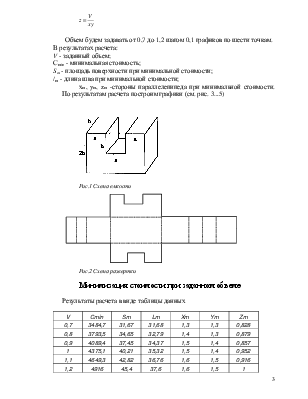
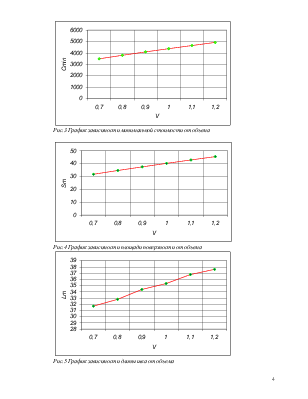
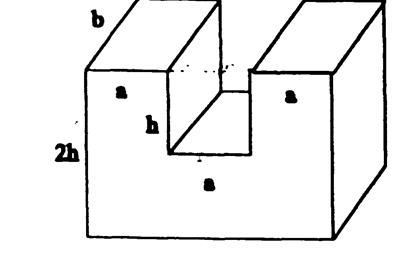
Спроектировать емкость заданного объема в заданной форме [см. рис. 1] при минимальной стоимости. Задана стоимость С₁ единицы площади материала и стоимость С₂ единицы  длины шва. Стоимость резания и изгибания материала не учитываются. Задача оптимального раскроя не решается, развертка фигуры приведена на рис. 2. Построить графики зависимостей минимальной стоимости площади поверхности и длины шва от объема.

Формализуем задачу:

Найти C_min=minC(x,y,z),

x,y,z

при х • у • z = V

х>0,у>0,z>0,

 где х, у, z- стороны параллелепипеда;

V - заданный объем.

Нужно найти явное выражение функции С от переменных x,у,z

С=С₁ •S+С₂•l,

где S - площадь поверхности;

/ - длина шва.

S=2(xy+xz+yt),

l=Z+2y+4x,

С(х, у, z) = 2С(ху + хz + уz) +С₂ (z + 2y + 4x).

Решать задачу будем наиболее простым методом оптимизации - методом сканирования. Переменная х изменяется от х₀ доx₁  шагом h_x ,

 у - от у_о до y₁ шагом h_y , переменная z зависит от х и у и заданного

объема:

              

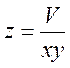
Объем будем задавать от 0,7 до 1,2 шагом 0,1 графиков по шести точкам.

В результатах расчета:

V - заданный объем;

С_min - минимальная стоимость;

S_m - площадь поверхности при минимальной стоимости;

/_m - длина шва при минимальной стоимости;

х_m, y_m, z_m -стороны параллелепипеда при минимальной стоимости. По результатам расчета построим графики (см. рис. 3...5)

Рис.1 Схема емкости

 

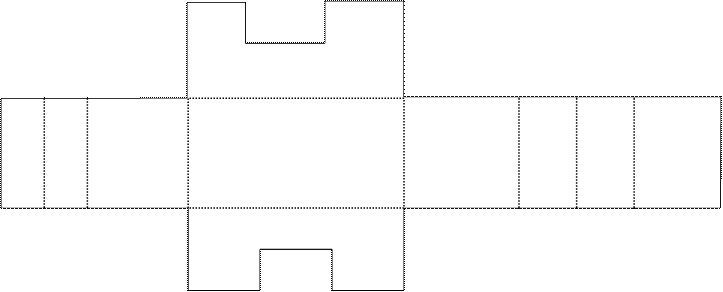Рис.2 Схема развертки

Минимизация стоимости при заданном объеме

Результаты расчета в виде таблицы данных

V	Cmin	Sm	Lm	Xm	Ym	Zm
0,7	3484,7	31,67	31,68	1,3	1,3	0,828
0,8	3793,5	34,65	32,79	1,4	1,3	0,879
0,9	4089,4	37,45	34,37	1,5	1,4	0,857
1	4375,1	40,21	35,32	1,5	1,4	0,952
1,1	4649,3	42,82	36,76	1,6	1,5	0,916
1,2	4916	45,4	37,6	1,6	1,5	1

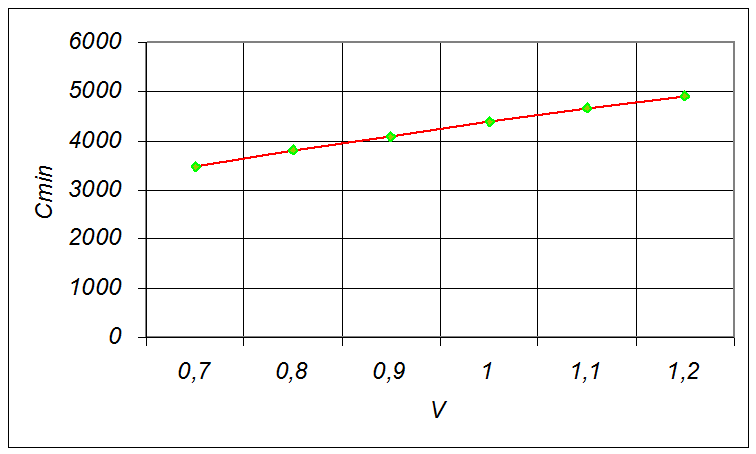
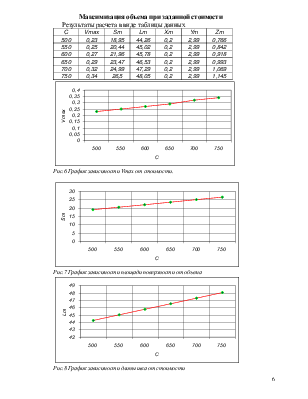
Рис.3 График зависимости минимальной стоимости от объема

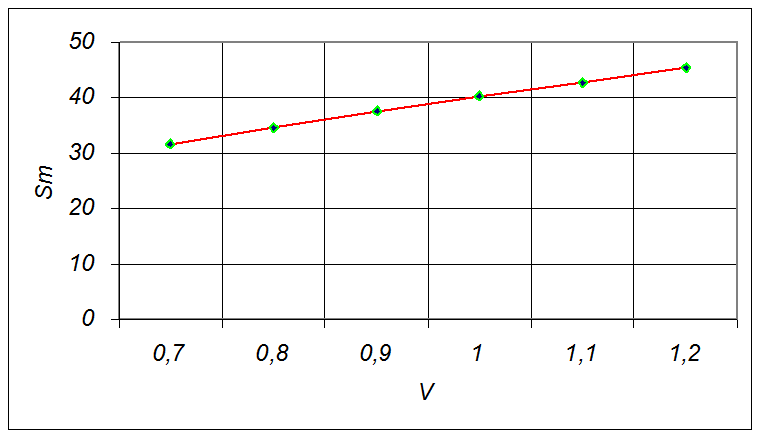
Рис.4 График зависимости площади поверхности от объема

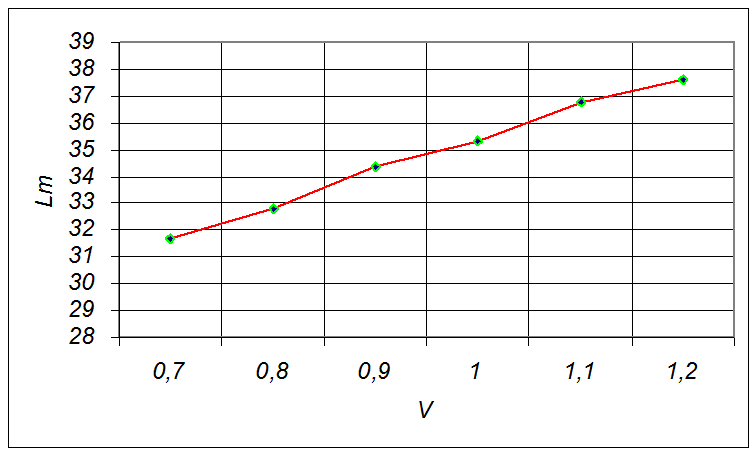
Рис.5 График зависимости длины шва от объема

2.  ЗАДАЧА ПАРАМЕТРИЧЕСКОЙ ОПТИМИЗАЦИИ ПРИ ПРОЕКТИРОВАНИИ ЕМКОСТИ МАКСИМАЛЬНОГО ОБЪМА ПРИ ЗАДАННОЙ СТОИМОСТИ

2.1.  ЦЕЛЬ РАБОТЫ:

Научиться делать постановку простых задач параметрического синтеза на примере проектирования емкости максимального объема при заданной стоимости, освоить использование программной системы TurboC, уметь написать и отладить программу на языке С⁺⁺ и получить конкретные результаты на ПК.

2.2.  ЗАДАНИЕ:

Спроектировать емкость максимального объема в заданной форме [см. рис. 1] при заданной зависимости С. Задана стоимость С₁ единицы площади материала и стоимость С₂ единицы  длины шва. Построить графики зависимостей максимального объема, площади поверхности и длины шва от заданной стоимости.

Формальная запись задачи:

НайтиV_max =maxV(x,y,z)

                        x,y,z

при 2C₁(xy + xz + yz) + С₂(z + 2у + 4x) = С,

х>0,y>0, z>0,

где х, у, z - стороны параллелепипеда;

С - заданная стоимость.

  Явное выражение функции V от переменных х, у, z

Изменяя переменные х и у, а переменную z находим из условия заданной стоимости

                     

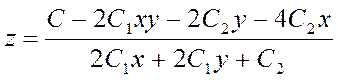
Стоимость будем .задавать от 500 до 750 шагом 50 - для построения графика по 6 точкам.

В результатах расчета:

С- заданная стоимость;

Vтах- максимальный объем;

Sm - площадь поверхности при максимальном объеме;

Lm - длина шва при максимальном объеме;

Хт,Ут,Ztm- стороны параллелепипеда при максимальном объеме.

Максимизация объема при заданной стоимости

Результаты расчета в виде таблицы данных

С	Vmax	Sm	Lm	Xm	Ym	Zm
500	0,23	18,95	44,26	0,2	2,99	0,766
550	0,25	20,44	45,02	0,2	2,99	0,842
600	0,27	21,96	45,78	0,2	2,99	0,918
650	0,29	23,47	46,53	0,2	2,99	0,993
700	0,32	24,99	47,29	0,2	2,99	1,069
750	0,34	26,5	48,05	0,2	2,99	1,145

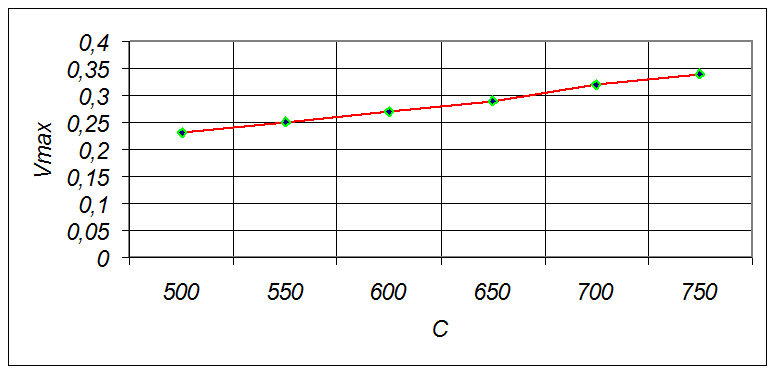
Рис.6 График зависимости Vmax от стоимости.

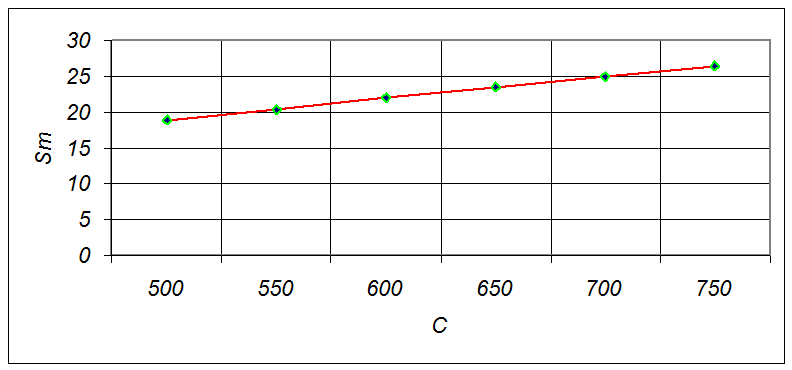
Рис.7 График зависимости площади поверхности от объема

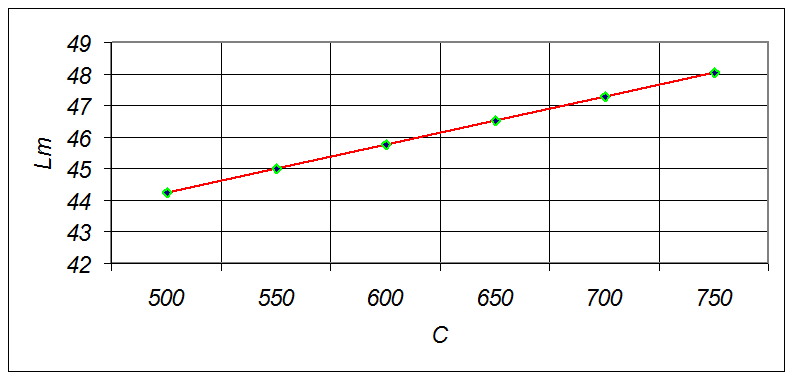
Рис.8 График зависимости длины шва от стоимости