С помощью критерия Стьюдента осуществляется проверка равенства математического ожидания формируемого случайного процесса v(t) заданной величине m0. Для этого вычисляется следующее отношение:
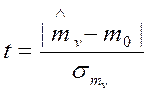 ,
,
где ![]() –
среднеквадратическое отклонение оценки математического ожидания.
–
среднеквадратическое отклонение оценки математического ожидания.
Значение среднеквадратического отклонения оценки математического ожидания равно:
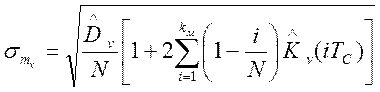 .
.
Вычисленное значение t сравнивалось с табличным tq,n для распределения Стьюдента, где q – уровень значимости риска, а V – число степеней свободы, которое вычисляется по соотношению:
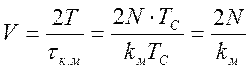 ,
,
где T – длина реализации v(t); tк.м – максимальный интервал корреляции.
Отличие оценки
математического ожидания ![]() от значения
от значения ![]() считается несущественным, если t < tq,n. Критерий F(Фишера)
здесь применяется для проверки равенства текущих значений дисперсии моделируемого
случайного процесса v(t) с заданной величиной D0. С этой целью вычисляется отношение:
считается несущественным, если t < tq,n. Критерий F(Фишера)
здесь применяется для проверки равенства текущих значений дисперсии моделируемого
случайного процесса v(t) с заданной величиной D0. С этой целью вычисляется отношение:
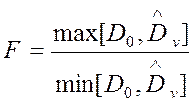 ,
,
где 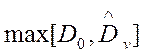 ,
, 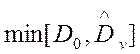 – соответственно максимальная и
минимальная из дисперсий.
– соответственно максимальная и
минимальная из дисперсий.
Вычисленное значение F
сравнивается с табличным Fтабл при данном для каждой
дисперсии числе степеней свободы и избранном уровне значимости риска. Число
степеней свободы для заданной дисперсии D0 принимается равным
бесконечности, а для текущих значений дисперсии, ![]() ,
принимается равным текущему значению случайного процесса n(t). В случае если F < Fтабл
различие между дисперсиями можно считать несущественным.
,
принимается равным текущему значению случайного процесса n(t). В случае если F < Fтабл
различие между дисперсиями можно считать несущественным.
Проверка равенства текущей
скорости изменения моделируемого случайного процесса заданной величине a0 осуществляется путем анализа совпадения
значений корреляционных функций ![]() и
и 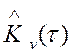 при заданном временном сдвиге tк.0.5. Интервал времени tк.0.5 принимается равным
при заданном временном сдвиге tк.0.5. Интервал времени tк.0.5 принимается равным ![]() при условии, что
при условии, что 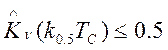 .
Значение нормированной корреляционной функции
.
Значение нормированной корреляционной функции ![]() вычисляется
по формуле:
вычисляется
по формуле:
![]() .
.
Равенство коэффициентов
корреляции ![]() и
и 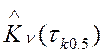 проверяется
с помощью критерия t.
Для чего вычислялось отношение:
проверяется
с помощью критерия t.
Для чего вычислялось отношение:
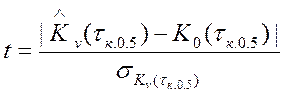 ,
,
где ![]() –
среднеквадратическое отклонение оценки значения
–
среднеквадратическое отклонение оценки значения 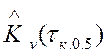 нормированной
корреляционной функции. Значение
нормированной
корреляционной функции. Значение ![]() в последнем выражении
равно:
в последнем выражении
равно:
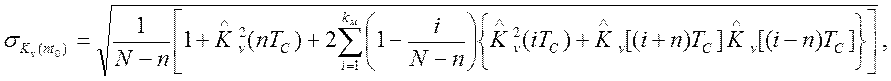
где 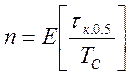 -
взятие операции определения целой части числа.
-
взятие операции определения целой части числа.
Вычисленное значение t-критерия сравнивается с табличным tq,n для распределения Стьюдента. И если скорость изменения моделируемого случайного процесса, α(t), отличается от заданной скорости, a0 , несущественно (если t < tq,n.), то математическое ожидание, дисперсия и скорость изменения моделируемых реализаций отличаются от этих характеристик экспериментальных реализаций так же несущественно.
4.4.2 Методические погрешности процесса управления
Прежде чем выходить на
стенд необходимо получить предварительные оценки статистических характеристик
объекта исследования и получить модели измерительной информации. Это делается
следующим образом. На первом шаге методики, экспериментально оценивается
скорость изменения технологического параметра. По реализации сигнала
рассчитываются статистические характеристики: математическое ожидание (![]() ), дисперсия (
), дисперсия (![]() ) и
корреляционная функция (
) и
корреляционная функция (![]() ) по формулам:
) по формулам:
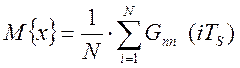 ,
,
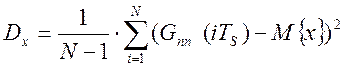 ,
,
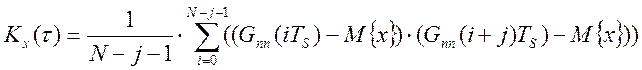 .
.
На рисунке 4.24 изображена
корреляционная функция управляющего сигнала «расход перегретого пара»
полученная в работе [6]. Математическая модель (кривая 2 на рис. 4.25) этой измерительной
информации, полученная аппроксимацией экспериментальной корреляционной функции
(кривая 1 на рисунке 4.25), имеет вид: ![]() .
.
На втором шаге методики выбираются элементы канала обработки информации. По каталогам выбираются конкретные технические средства для реализации измерительного канала. Из инструкций по эксплуатации нации выбранных технических средств извлекаются математические модели характеристик элементов измерительного канала.
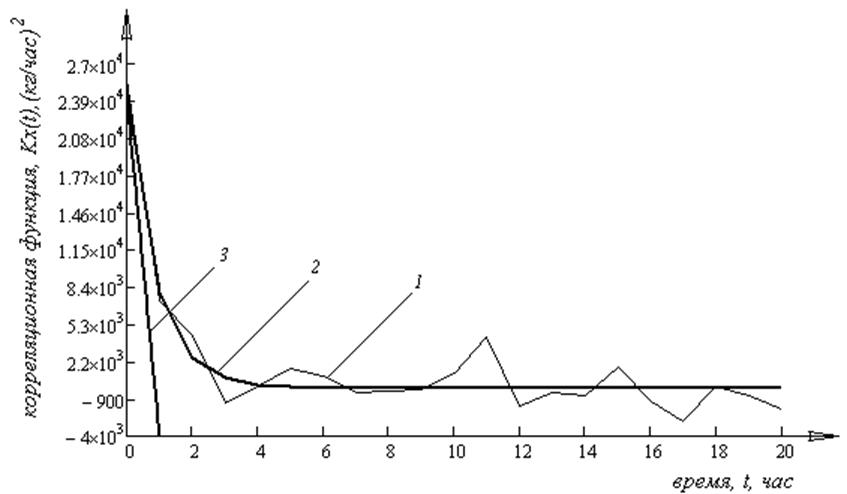
Рисунок 4.25 1 – корреляционная функция, искаженная помехой; 2 – модель корреляционной функции; 3 – касательная, проведенная к модели.
Для измерения
расхода перегретого пара, рассматриваемого в работе [6] это: уравнение
измерения чувствительного элемента ![]() ; первичный
преобразователь с динамической характеристикой:
; первичный
преобразователь с динамической характеристикой: 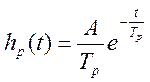 и
динамическая характеристика программного компенсатора:
и
динамическая характеристика программного компенсатора: 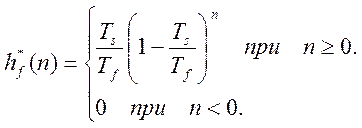
На третьем шаге
методики проводится предварительная оптимизация настроечных коэффициентов
программного обеспечения по моделям представленным на рисунках 4.26 -:- 4.28 [9].
Сначала, по скорости изменения сигналов, α, определяется величина относительной
динамической методической составляющей погрешности обработки информации в
измерительной системе, ![]() . При этом выбирается и общий
темп обработки информации в измерительной системе, TS (см. рис. 4.26).
. При этом выбирается и общий
темп обработки информации в измерительной системе, TS (см. рис. 4.26).
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.