Кроме
того, проверка соответствия математического ожидания отклонений ![]() , оценке отклонений
, оценке отклонений ![]() , осуществлялась с помощью критерия Фишера.
Для этого вычислялось отношение:
, осуществлялась с помощью критерия Фишера.
Для этого вычислялось отношение:
|
Проверка
соответствия значения дисперсии |
Где ![]() ,
, ![]() - соответственно максимальное
отклонение и минимальное отклонение. Здесь оценка дисперсии вычислялась по
выражению:
- соответственно максимальное
отклонение и минимальное отклонение. Здесь оценка дисперсии вычислялась по
выражению:
|
|
Вычисленное значение критерия Фишера сравнивалось с табличным при
уровне значимости риска равном 0,05. Число степеней свободы для теоретического
значения дисперсии динамической погрешности ![]() принималось
равным количеству варьируемых коэффициентов (
принималось
равным количеству варьируемых коэффициентов (![]() и
и ![]() соответственно). Для оценки дисперсии
соответственно). Для оценки дисперсии ![]() , вычисленной по результатам эксперимента,
число степеней свободы принималось равным:
, вычисленной по результатам эксперимента,
число степеней свободы принималось равным:
|
|
Если расчётное значение критерия Фишера оказывалось меньше
табличного, то различие между дисперсиями ![]() и
и ![]() можно считать несущественным, а
математическую модель адекватной по дисперсии.
можно считать несущественным, а
математическую модель адекватной по дисперсии.
На рисунке 4.20 показана одна из экспериментальных реализаций, полученных с помощью стенда [29]. Здесь показания полевого прибора [30] показаны сплошной линией (блок 15 на рисунке 4.20), а показания эталонного вычислителя (см. блок 8 на рисунке 4.20) показаны пунктирной линией.
|
|
Рис. 4.21 Экспериментальные реализации стенда [29]
4.4.1 Проверка адекватности моделей измерительной информации
Проверка алгоритмов визуализации процессов измерения и управления может проводиться на стенде для диагностики программного обеспечения систем управления (СДПСУ). Внешний вид стенда представлен на рисунке 4.22 и [29].
Для решения задач диагностики программного обеспечения робастных систем создано специальное программное обеспечение стенда – это пакет прикладных программ ППП «СДПСУ, функциональная схема информационных потоков в котором, изображена на рисунке 4.23.
ППП «СДПСУ» функционирует следующим образом. Истинные значения измеряемой величины, X(t), и помехи, N(t), моделируются в блоке 1 по алгоритмам, которые подробно описаны в работах [23, 58, 64]. Сигнал с аддитивной помехой: X(t)+N(t), преобразуется в аналоговый с помощью блока 5 и возвращается в ЭВМ общего назначения, посредством блока 6. Прошедший двойную дискретизацию сигнал, Z(t), после предварительной обработки в блоках 4 и 3, поступает на визуализацию в блок 2.
На рисунке 4.24 изображен фрагмент работы алгоритма визуализации процесса измерения истинного значения, X(t). На рисунке 4.23 жирной линией отображается моделируемая синусоида, тонкая ступенчатая линия отображает сигнал, искажённый помехой, а жирная ступенчатая линия отображает процесс формирования методической динамической ошибки цифровой обработки измерительной информации: E(t)=X(t)-Z(t).

.
Рис. 4.22 Внешний вид стенда для диагностики программного обеспечения.
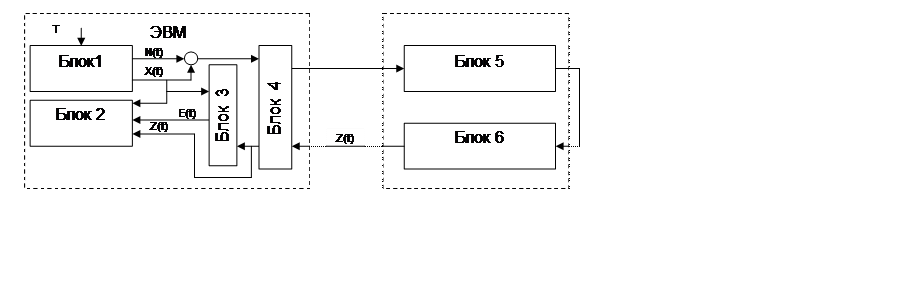
Рис. 4.23 Схема информационных потоков стенда
Поверка гипотез осуществляется следующим образом: вычисляется предварительная оценка математического ожидания случайного процесса v(t):
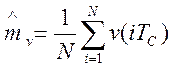 ,
,
где N – количество отсчетов реализации v(t); TC – интервал времени между двумя соседними отсчетами реализации случайной функции v(t). При этом длина реализации T=NTC выбиралась как можно больше.
Вычисляются предварительные оценки значений нормированной корреляционной функции:
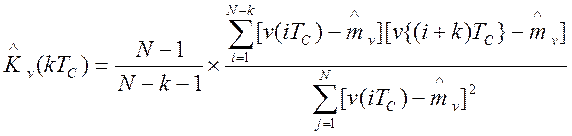 ,
,
где k=0, 1, 2 … , l; l£ 0.1N.
Расчет значений
нормированной корреляционной функции осуществляется до значения kм,
при котором 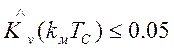 . Значения функции v(t) через
интервал корреляции
. Значения функции v(t) через
интервал корреляции ![]() считаются некоррелированными, а
так как процесс нормальный, то и статистически независимыми.
считаются некоррелированными, а
так как процесс нормальный, то и статистически независимыми.
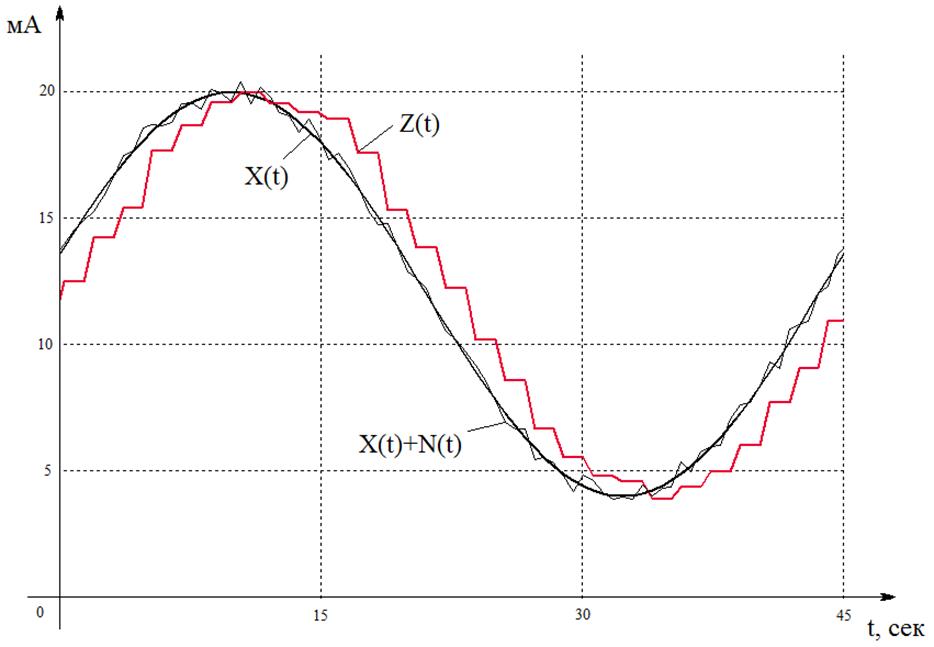
Рис. 4.24. Визуализация динамических погрешностей в процессе измерения
Далее формируется новая реализация длиной T=tк.м×102. Оценки статистических характеристик, рассчитываемые по реализации такой длины имеют распределение близкое к нормальному. Интервал времени TC между соседними отсчетами принимается равным tк.м/100.
По новой реализации
вычисляется уточненные оценки математического ожидания ![]() ,
значений нормированной корреляционной функции
,
значений нормированной корреляционной функции 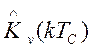 и
интервала корреляции tк.м. Кроме
того, вычисляется оценка дисперсии:
и
интервала корреляции tк.м. Кроме
того, вычисляется оценка дисперсии:
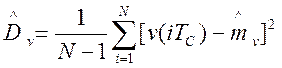 .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.