Изохорное нагревание воды и водяного пара (Лабораторная работа № 4)

Цель работы: ознакомление студентов с термодинамическими свойствами рабочих тел на примере воды и водяного пара. Освоение методики опытного определения зависимости между давлением и температурой в двухфазной области и процессе изохорного нагревания. Освоение способа нахождения теплоты парообразования.

Краткие сведения из теории

Всякое вещество может находиться в разных фазах, которые представляют собой различные агрегатные состояния вещества. Фаза – это однородная система с одинаковыми физическими свойствами во всех её частях. Характерная особенность фаз – наличие границ.

В ходе лабораторной работе мы рассматриваем систему вода – водяной пар. На диаграмме давления от температуры она представлена кривой Р=Р(Т).

 Однако, при переходе через кривую не всегда происходит фазовый переход и вещество остается в одной фазе, не распадаясь, такое состояние называется метастабильным. Это объясняется устойчивостью фаз. 

При изотермическом равновесном переходе через границу фазы 1 кг вещества происходит поглощение (или выделение) теплоты, которое называется удельной теплотой фазового перехода.

Изменение давления вдоль кривой равновесия, или, что тоже самое, зависимость равновесного давления обеих фаз от температуры определяется по формуле Клайперона-Клаузиуса:

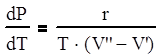
где dP/dT – производная от давления по температуре, взятая по кривой фазового равновесия;

r – удельная теплота фазового перехода;

V` - удельный объем воды при температуре кипения;

V`` - удельный объем сухого пара.

При малых давлениях удельным объемом кипящей воды можно пренебречь:

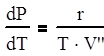
Зная зависимость давления от температуры и удельный объем сухого пара, можно узнать удельную теплоту парообразования.

При малых давлениях будем считать зависимость теплоты парообразования ( r) от температуры – линейная функция:

состояние сухого пара описывается уравнением, близким к уравнению состояния идеального газа:

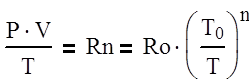
Постоянная n находится по известной из опыта совокупности соответствующих величин Р, Т и V. Как показали расчеты, в интересующим нас диапазоне давлений можно принять n = 0,14. Получим дифференциальное уравнение для единственной неизвестной постоянной с:

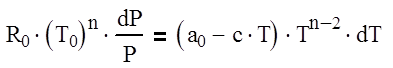
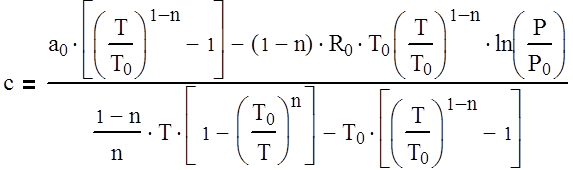
В выбранном диапазоне давлений можно принять с = 2,7.

Теперь, когда обе постоянные известны, можно вычислить удельную теплоту парообразования – конденсации в любой точке интересующего нас отрезка кривой насыщения.

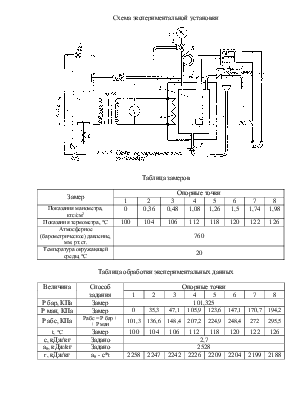
Схема экспериментальной установки

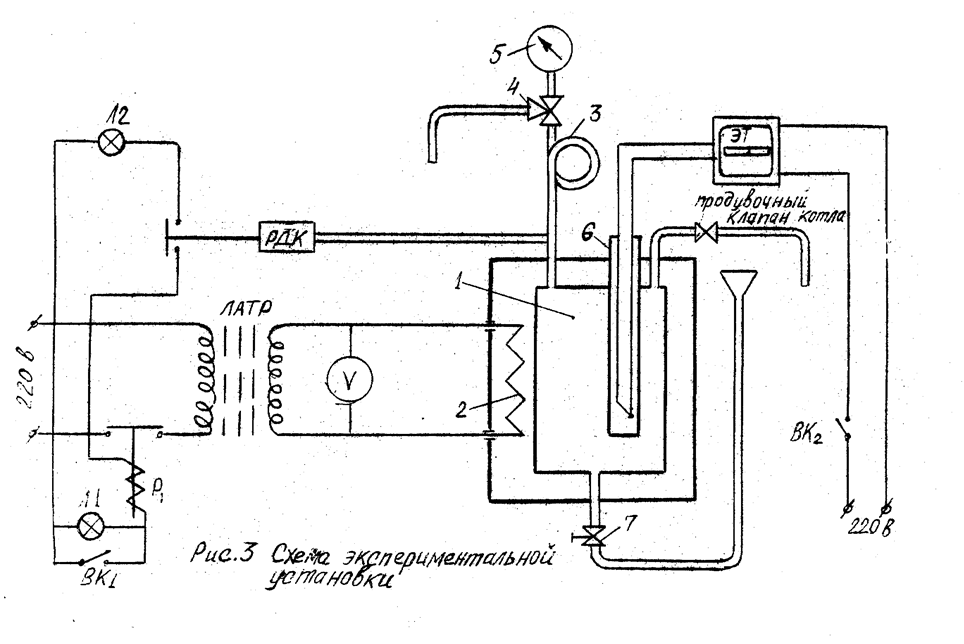
Таблица замеров

Таблица обработки экспериментальных данных