Цель работы: ознакомиться с методикой экспериментального определения показателя адиабаты для воздуха.
1. ОБЩИЕ СВЕДЕНИЯ.
Адиабатным называется процесс изменения состояния рабочего тела без подвода и отвода теплоты.
Графически такой процесс изображается линией, которая называется адиабатной.
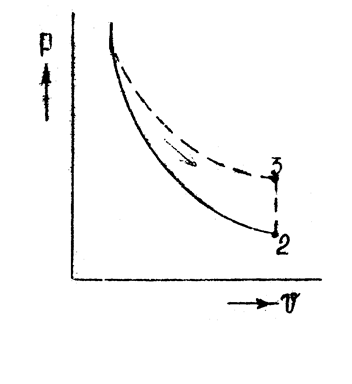
рис 1
На pv – диаграмме линия 1-2 (рисунок 1) представляет собой гиперболу. Уравнение адиабаты имеет вид pvk = const. Здесь k – показатель адиабаты (величина, равная отношению изобарной теплоёмкости к изохорной): k = Cp/Cv. Это отношение зависит от температуры вещества, но для газов и паров эта зависимость настолько мала, что ею в расчётах часто пренебрегают, принимая k величиной постоянной. В таких случаях принимают это отношение равным для идеальных газов: одноатомных – 1.67; двухатомных – 1.4; трёх- и многоатомных – 1.29. Точные значения k для некоторых газов и водяных паров в зависимости от температур приведены в справочных данных.
2. ОПИСАНИЕ ЭКСПЕРИМЕНТАЛЬНОГО СТЕНДА И ПРОЦЕССОВ, ПРОИСХОДЯЩИХ ВО ВРЕМЯ ОПЫТОВ.
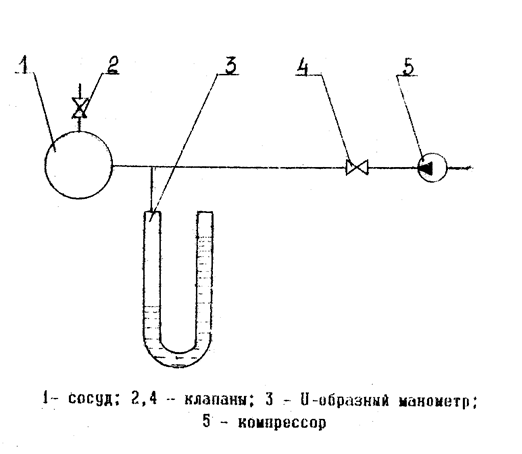
Стальной сосуд 1 может попеременно сообщаться при помощи клапанов 2 и 4 либо с атмосферой, либо с компрессором 5. Абсолютное давление воздуха в сосуде определяется как сумма барометрического давления и избыточного, измеряемого U – образным манометром.
Допустим, что воздух в сосуде имеет начальные параметры P1, V1, T1, причём температура T1 равна температуре окружающей среды, а давление P1 выше атмосферного.
Это состояние изобразится на диаграмме P – V (рисунок 1) точкой 1. Если сообщить сосуд с атмосферой, то воздух вытечет из него и расширится до атмосферного давления. Процесс расширения 1-2 происходит очень быстро, поэтому с известным приближением его можно считать протекающим без теплообмена с окружающей средой, т.е. адиабатным. В точке 2 давление P2 равно атмосферному, температура T2 ниже начальной. В момент, когда давление воздуха понизится до атмосферного, сосуд закрывается, и далее происходит изохорный процесс 2-3, при котором температура воздуха повышается за счёт теплообмена через стенки сосуда до температуры окружающей среды. В точке 3 температура T3 = T1, давление P3 несколько превышает атмосферное. На рис.1 через точки 1 и 3 условно проведена изотерма T = const.
3. МЕТОДИКА ПРОВЕДЕНИЯ ИСПЫТАНИЙ И ОБРАБОТКА РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТОВ.
В начале опыта при замкнутом клапане 2 и открытом клапане 4 с помощью компрессора создаётся в сосуде избыточное давление в пределах 1000…1300 мм.рт.ст. Так как температура воздуха в сосуде повышается, необходимо подождать 5…7 мин, пока температура не понизится до температуры окружающей среды. После выравнивания температуры, о чём можно судить по стабилизации уровней в манометре, производят отсчёт избыточного давления Pман1. Затем открывают клапан 2 на короткое время, за которое давление в сосуде резко падает до атмосферного, и одновременно понижается температура. Далее снова необходимо подождать, пока произойдёт выравнивание температуры внутри и снаружи закрытого сосуда (об этом можно судить по стабилизации уровня в манометре). Когда давление в сосуде устанавливается, производят отсчёт избыточного давления Pман3.
Опыт следует повторить 4 раза, меняя каждый раз величину Pман1.
Для каждого опыта величина k определяется по формуле:
K = Pман1/(Pман1 – Pман3),
где Рман1 и Pман3 – избыточное давление в точках 1 и 3.
Величину k находят как среднее арифметическое значение из полученных величин k1. Погрешность в определении оценивается по отклонению величины kср от известного теоретического значения kт = 1.4 для воздуха.
ОПЫТНЫЕ ДАННЫЕ
|
Номер опыта |
Pман1, мм.вод.ст. |
Pман3, мм.вод.ст. |
Pман1/Pман1- Pман3 |
|
1 2 3 4 |
19 16 15 18 |
4.2 3.8 3.5 4 |
1.284 1.311 1.304 1.286 |
K1 = 19/19 – 4.2 = 1.284
K2 = 16/16 – 3.8 = 1.311
K3 = 15/15 – 3.5 = 1.304
K4 = 18/18 – 4 = 1.286
Средняя величина kср составляет:
Kср = K1+K2+K3+K4/4,
Kср = 1.284+1.311+1.304+1.286/4 = ~1.3
Рассчитываем погрешность
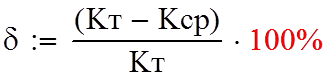
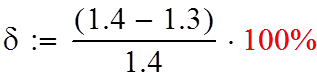
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.