1.
Отримати для даної функції МДНФ за методом Вейча
|
|
f( |
|
0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 |
0 1 0 1 0 1 0 1 0 0 0 0 0 0 1 1 |
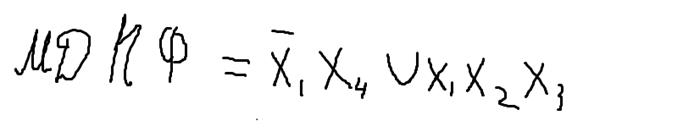 V x2x3x4
V x2x3x4
2.
Отримати для даної функції МДНФ за методом Квайна
|
|
f( |
|
0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 |
0 1 0 1 0 0 0 0 0 1 0 0 0 0 1 1 |
МДНФ має вигляд:



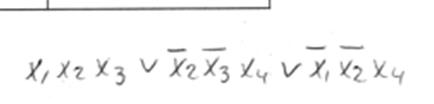
3.
Який вигляд має
поліном Жегалкіна для функції ![]() ?
?



Xyz +xz+xy+x+y+z+yz
4.
Розбити стани q![]() автомата на класи еквівалентних станів за
алгоритмом Мілі
автомата на класи еквівалентних станів за
алгоритмом Мілі
Вхідний алфавіт A(a![]() , a
, a![]() , a
, a![]() ) і
вихідний алфавіт V(v
) і
вихідний алфавіт V(v![]() ,v
,v![]() ,)
,)
|
q |
a |
|
1 2 3 4 5 6 7 8 9 |
2.0 4.1 4.1 1.1 1.0 5.0 1.1 6.0 5.0 8.0 1.1 1.1 6.1 4.1 3.0 8.0 9.1 6.1 6.1 1.1 3.0 4.1 4.0 7.0 7.0 9.1 7.1 |
Розбиття
станів q![]() на класи еквівалентних станів має вигляд
на класи еквівалентних станів має вигляд



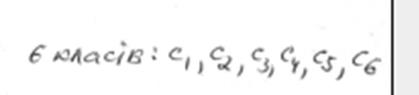
5
Розбити стани q![]() автомата на класи еквівалентних станів за
алгоритмом Мілі
автомата на класи еквівалентних станів за
алгоритмом Мілі
Вхідний алфавіт A(a![]() , a
, a![]() , a
, a![]() ) і
вихідний алфавіт V(v
) і
вихідний алфавіт V(v![]() ,v
,v![]() ,)
,)
|
q |
a |
|
1 2 3 4 5 6 7 8 |
3.1 2.0 4.0 2.1 1.1 4.0 1.1 5.0 6.0 2.0 1.1 8.1 5.1 1.1 4.0 2.0 3.1 7.1 4.1 3.0 1.0 6.1 1.0 1.0 |
Розбиття станів q![]() на класи еквівалентних станів має вигляд
на класи еквівалентних станів має вигляд
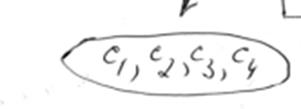
6
Розбити стани q![]() автомата на класи еквівалентних станів за
алгоритмом Мілі
автомата на класи еквівалентних станів за
алгоритмом Мілі
Вхідний алфавіт A(a![]() , a
, a![]() , a
, a![]() ) і
вихідний алфавіт V(v
) і
вихідний алфавіт V(v![]() ,v
,v![]() ,)
,)
|
q |
a |
|
1 2 3 4 5 6 7 8 |
2.0 5.0 3.1 1.0 1.1 1.0 3.1 7.1 2.1 5.1 1.1 6.1 8.0 1.0 3.1 7.1 3.1 2.1 3.1 6.0 1.1 1.0 5.1 1.0 |
Розбиття станів q![]() на класи еквівалентних станів має вигляд
на класи еквівалентних станів має вигляд
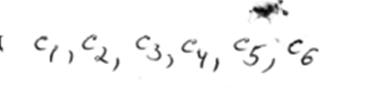
7.
Який вигляд має
поліном Жегалкіна для функції ![]() ?
?
![]()
Xz+yz+x+z
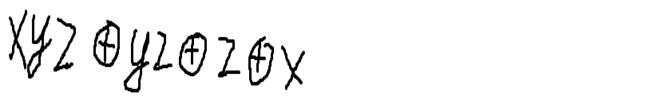 b
b
8.
Отримати для даної функції МДНФ за методом Вейча
|
|
f( |
|
0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 |
0 1 0 1 0 0 0 0 0 1 0 0 0 0 1 1 |
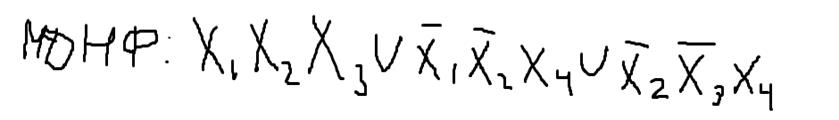 j
j
9.
Перевірити дану функцію на не монотонність і
виразити через неї заперечення ![]()
|
|
f( |
|
0 0 0 0 0 0 0 1 0 0 1 0 0 0 1 1 0 1 0 0 0 1 0 1 0 1 1 0 0 1 1 1 1 0 0 0 1 0 0 1 1 0 1 0 1 0 1 1 1 1 0 0 1 1 0 1 1 1 1 0 1 1 1 1 |
0 1 0 1 0 0 0 0 0 1 0 0 0 0 1 1 |
![]() дорівнює:
дорівнює:

Функция немонотонна
10.
Який вигляд має
поліном Жегалкіна для функції ![]() ?
?
Xy+xz+z
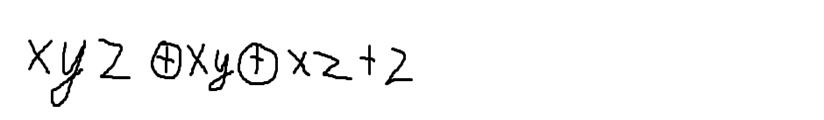 j
j
11.
Нехай p,q,r визначають слідуючи висловлення :
p: Він купить комп’ютер;
q: Він буде святкувати всю ніч;
r: Він виграє в лотерею.
Запишіть наступне висловлення, що представлено символьним виразом:
![]() .
.
Якщо він виграє в лотерею, то він купить компьютер і буде святкувати всю ніч
12.
Відома множина А={a,b}.Знайти чому дорівнює А2.
aa,ab,ba,bb
13.
Знайти мінімальну ДНФ для функції f(x,y,z)=![]() ?
?
![]()
14.
Вкажіть кількість всіх підмножин множини {§,¨,©}?
8
15.
Сформулюйте теорему Ейлера з теорії графів
Связный граф является эйлеровым тогда и только тогда когда степени всех его вершин четны
16.
Дайте визначення поліному Жегалкіна, що застосовується в математичній логіці


P=a0+a1x1+a2x2+…+anxn+…+a2n-1x1x2…xn
17.
Яка операція на множині називається бінарною?
Обьединение
Пересечение
разность
18.
Нехай заданий двомісний предикат P(x,y) : «x любить y». Як за допомогою логіки предикатів представити фразу – « Кожну людини хтось любить» ?
Для любого у существует такой х что P(x,y)
19.
Що називають деревом в теорії графів?
Связный ацикличный ориентированный граф
20.
Що складає сигнатуру алгебраїчної системи?
Сукупність предикатів або множина алгебраїчних оперцій непустої множини і множина відношень визначених на А
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.