Порівняння диференціальної та ануїтетної схем кредитування

Теоретична частина

Позичковий капітал є важливим параметром керування у сучасних бізнес-процесах. Різні типи кредитних відносин між кредитором (банком) та боржником (фірмою) виникають через різні схеми погашення боргу.

Нехай  – сума кредиту, що береться на  місяців за річною процентною ставкою . Кожного -го місяця () боржник повинен виплачувати кредит  деякими частинами  (база кредиту), а також величину  за користування ним (проценти). Якщо проценти нараховуються на всю суму кредиту , то

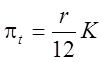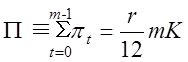                              , .                      (1.1)

Такі проценти називають простими і скоріше використовують у депозитних, ніж кредитних зобов’язаннях. Сучасні кредити надаються під складні проценти, суть яких полягає в тому, що вони нараховуються не на всю суму боргу , а на його поточний залишок  на початок місяця . Розглянемо найпоширеніші на практиці схеми кредитування за складними процентами: диференціальну та ануїтетну.

            Диференціальна схема (від англ. differential – різний, відмінний) передбачає виплату суми боргу  рівними частинами при нарахуванні процентів на залишок боргу :

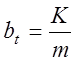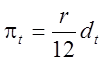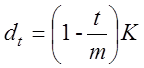             , , , .     (1.2)

Тим самим сума щомісячної виплати  буде різною. Звідси й назва такої схеми кредитування.

            Ануїтетна схема (від англ. annuity – рівні фінансові виплати) передбачає виплату суми боргу  різними частинами при нарахуванні процентів на поточний залишок боргу  за умови незмінності щомісячної виплати . Задовольняючи систему умов

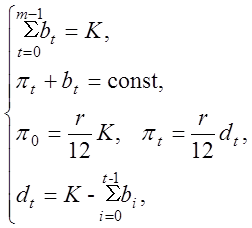                                                              (1.3)

приходимо до таких формул для ануїтетної схеми кредитування ():

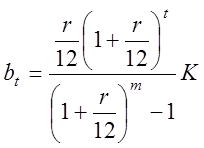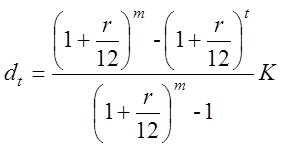             ,   .     (1.4)

У цьому випадку, як і для диференціальних виплат,

.

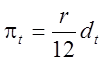Також можна отримати формулу для розрахунку щомісячної виплати по ануїтетному кредиту.

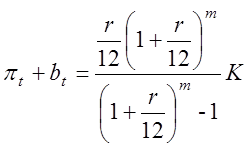                                   .                           (1.5)

Зауважимо, що при  формула (1.5) набуває вигляду

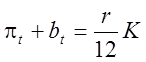                                                                                (1.6)

і є формулою для безстрокового ануїтету, або перпетуїтету
(від англ. perpetual – вічний, нескінченний). Перпетуїтети часто застосовуються при обчисленні дивідендів, купонів по облігаціях та інших фінансових розрахунках. У кредитуванні перпетуїтети на практиці не трапляються. Тому надалі вони будуть мати суто математичне значення.

Практична частина

Для порівняння диференціальної та ануїтетної схем кредитування провести аналіз математичних моделей (1.2) та (1.4).

 Вихідні дані:

1.  Побудувати розрахункові таблиці для обох моделей кредитування.