Побудова моделі вхід-вихід та моделі з простором станів. Дослідження проблеми керованості, досяжності, спостережуваності, стійкості та асимптотичної стійкості

Завдання За передатною функцією системи

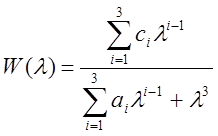           побудувати:

1)  модель вхід-вихід та  модель з простором станів;

2)  дослідити проблеми:

- керованості,  досяжності та спостережуваності;

- стійкості та асимптотичної стійкості;

3)  визначити потребу в декомпозиції системи.

Варіант 16

Варіант
16	3,72	8,25	1,46	-2,21	-3,72	8,21

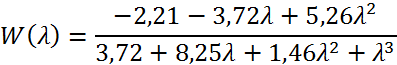
Модель вхід-вихід:

Загальний вигляд моделі:

 

В даному випадку , тоді:

Модель з простором станів:

Дискретна стаціонарна лінійна детермінована модель із простором станів має вигляд:

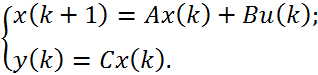
 В даному випадку:

 

 

 

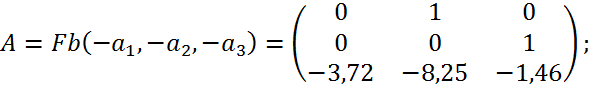
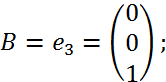
Дослідити на керованість:

Система є керованою, якщо можна організувати такий вхід в систему, який би дозволив отримати очікуваний вихід.

За умовою повної керованості ––  критерієм Калмана:

.

В даному випадку  повинен дорівнювати три:

> with(LinearAlgebra):

> A := <<0|1|0>,<0|0|1>,<-3.72|-8.25|-1.46>>;

> B := <0,0,1>;

> C := <-2.21|-3.72|8.21>;

>

>

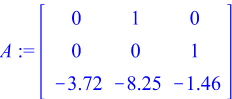
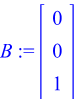
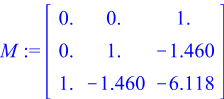
Оскільки  за критерієм Калмана система керована.

Дослідити систему на досяжність:

Для стаціонарних систем для повної досяжності необхідно і достатньо, щоб система була керованою.

Оскільки система керована (виконується критерій Калмана), то вона є і повністю досяжною.

Дослідити на спостережуваність:

Система спостережувана,  якщо:

.

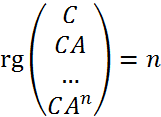В даному випадку ранг  повинен дорівнювати три:

>

>

Оскільки  система спостережувана.

Дослідити на асимптотичну стійкість:

Для асимптотичної стійкості системи необхідно і достатньо, щоб модулі всіх власних чисел матриці  були менше одиниці.

>

>

>

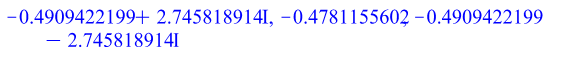
Умова не виконується, так як одне з власних чисел більше одиниці, це означає, що система не є асимптотично стійкою.

Дослідити на стійкість:

За критерієм стійкості Гуровиця: для того, щоб динамічна система була стійкою, необхідно і достатньо, щоб всі  діагональних мінорів матриці Гурвиця були додатні.

Матриця Гуровиця має вигляд:

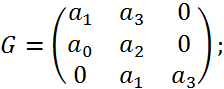
В даному випадку:

>

>

>

>

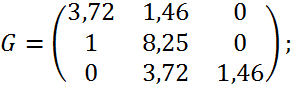
Оскільки всі діагональні мінори матриці Гурвиця додатні – система стійка.

Визначити потребу в декомпозиції системи:

Оскільки система керована і спостережувана, не має потреби в декомпозиції.