


Лабораторна робота №9
Рева М.В.
Iн-72
Варіант №15
За передатною функцією системи
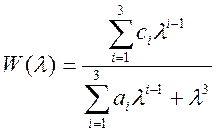 побудувати:
побудувати:
1) модель вхід-вихід та модель с простором станів;
2) дослідити проблеми:
- керованості; досяжності та спостережуваності;
- стійкості та асимптотичної стійкості;
|
Варіант |
|
|
|
|
|
|
|
15 |
7,18 |
-13,51 |
0,29 |
0,21 |
-4,45 |
5,26 |
Запишемо передатну функцію системи:
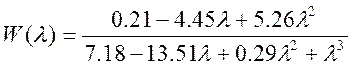
Побудуємо модель «Вхід-вихід»
Загальний вигляд моделі «Вхід-вихід»:
![]()
Маємо:
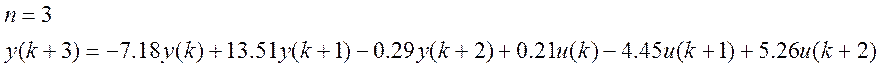
Дискретна стаціонарна лінійна детермінована модель з простором станів має, як відомо, вигляд
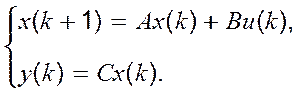 , де A=Fb(-a1, -a2, ... , -an), В=еп і С=(c1,c2,...,cn).
, де A=Fb(-a1, -a2, ... , -an), В=еп і С=(c1,c2,...,cn).
У нашому випадку матимемо:
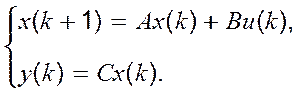 , де
, де
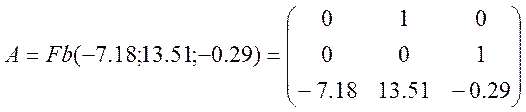
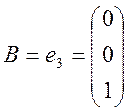 ,
, ![]() .
.
Порядок даної моделі ![]() .
.
Оскільки наша система є стаціонарною, тобто матриці A, B і C явно від часу не залежать, то критерій повної спостережуваності моделі має вигляд:
rg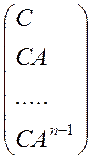 = n. (*)
= n. (*)
Тобто, система
спостережувана тоді і тільки тоді, коли ця умова виконується. Якщо ![]()
Достатня ж умова повної керованості (критерій Калмана) для стаціонарної моделі має вигляд:
rg(B, АВ,..., Аn-1B) = n (**)
Для асимптотичної стійкості системи необхідно і достатньо, щоб модулі всіх власних значень матриці А були менше одиниці.
> with(linalg):
A:=matrix([[0,1,0],[0,0,1],[-7.18,13.51,-0.29]]);
Warning, the protected names norm and trace have been redefined and unprotected
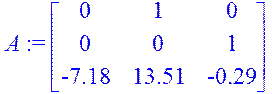
> B:=vector([0,0,1]);
![]()
> C:=vector([0.21,-4.45,5.26]);
![]()
> n:=3;
![]()
> det(A);
![]()
> AB:=multiply(A,B);
![]()
> A2B:=multiply(multiply(A,A),B);
![]()
> Matr:=concat(B,AB,A2B);
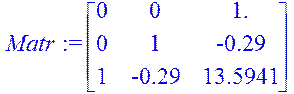
> rank(Matr);
![]()
> CA:=multiply(C,A);
![]()
> C2A:=multiply(C,multiply(A,A));
![]()
> Matr_:=stackmatrix(C,CA,C2A);
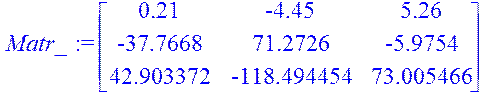
> rank(Matr_);
![]()
> Poly:=charpoly(A,x);
![]()
> Spectrum:=solve(Poly,x);
![]()
> Spectrum;
![]()
Отже з виконаних розрахунків видно, що умови
(*) і (**) виконуються, а значить дана модель є повністю керованою і повністю
спостережуваною. А оскільки ![]() і система
спостережувана, то вона є і досяжною. З іншого боку, умова
асимптотичної стійкості не виконується, а значить наша система не є
асимптотично стійкою.
і система
спостережувана, то вона є і досяжною. З іншого боку, умова
асимптотичної стійкості не виконується, а значить наша система не є
асимптотично стійкою.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.