Одержання моделі з простором станів із вхід-вихід моделі

Лабораторна робота №5

Тема: Одержання моделі з простором станів із вхід-вихід моделі

Завдання 4.5. За моделями вхід-вихід, знайденими за варіантами завдання 4.4 з таблиці 4.4 побудувати еквівалентні моделі з простором станів.

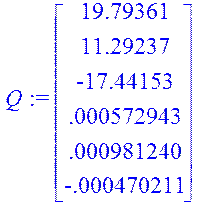
Теоретична частина

            (4.19)

Для систем зі скалярними входом і виходом задана модель

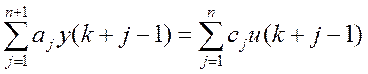, де a_n+1=1.

Будемо вважати, що поліноми

а₁+a₂λ+...+a_n+1λⁿ

і

 c₁+с₂λ+. . .+c_nλ^n-1

не мають спільних нулів. Дискретна стаціонарна лінійна детермінована модель з простором станів має, як відомо, вигляд

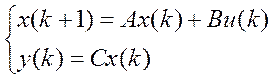.                      (4.22)

Стверджується, що така еквівалентна модель із простором станів може бути задана матрицями

A=Fb(-a₁, -a₂, ... , -a_n), В=е_п і С=(c₁,c₂,...,c_n).

Іншу модель із простором станів, що еквівалентна моделі (4.19), можна одержати за формулами

А=Fb*(-a), B=col(c₁, ..., c_n), C = e_n^*        (4.24)

Дійсно, у лівій частині вхід-вихід моделі, еквівалентної моделі (4.24), коефіцієнти дорівнюють коефіцієнтам полінома

Χ_A=det(λI–Fb*(-a))=det(λI–Fb(-a))*=a₁+a₂λ+...+a_nλ^n-1+λⁿ,

тобто збігаються з коефіцієнтами моделі (4.19).

Обчислимо коефіцієнти правої частини вхід-вихід моделі, що відповідає моделі з матрицями (4.24). Маємо

Cφ_j(A)B=e_n*φ_j(Fb^*(-a))col(с₁,...,с_n)=(φ_j(Fb(-a)e_n)*col(с₁,...,с_n)=e_j*col(с₁, ..., с_n) = c_j             (4.25)

тобто моделі (4.19) і (4.24) еквівалентні.

Хід роботи

Завдання 5.1 Дискретні моделі з простором станів, отримані в завданні 4.5, дослідити на керованість та спостережуваність

Для моделі з простором станів

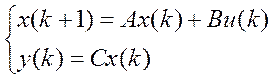
будуємо матриці

A=Fb(-a₁, -a₂, -a₃), В=е₃ і С=(c₁,c₂,c₃),

Використовуючи коефіцієнти заданої моделі вхід-вихід.

        

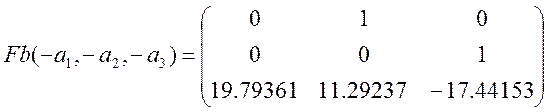
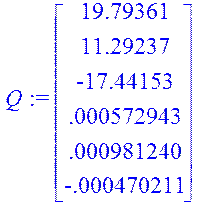
Перевірка на керованість.

Система (5.1) називається повністю k₀-керованою, якщо для будь-якого x⁰ існують k¹ = k₁(x⁰) < ∞ і керування u[k₀, k₁] ,що переводить цю систему зі стану х⁰ у стан x=0.

Теорема . Система (5.1) є повністю k₀-керованою, якщо існує k₁ < ∞ і виконується умова (5.6) або еквівалентна їй умова (5.8).

Розглянемо тепер випадок стаціонарних систем. У цьому випадку Ф(k₁, j) = A^k1-j, тому критерій (5.6) набуває вигляду

rg(A^k1-k0-1B,…,AB,B)=n                       (5.9)

x(k +1) = A(k)x(k) + B(k)u(k) + ƒ(k),                           (5.1)

rgV(k₀, k₁) = п                                                  (5.6)

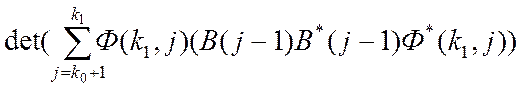≠0      (5.8)

Відповідно до цього, щоб наша система була керованою необхідно і достатньо (за критерієм Калмана) щоб

У нашому випадку , тому система є керованою

Перевірка на спостережуваність.

Система (5.1), (5.2) називається повністю k₀ спостережуваною на [k₀,k₁] якщо між її станами x(k₀) і виходами y[k₀,k₁] існує взаємно-однозначна відповідність.

Для випадку стаціонарної системи Критерій повної спостережуваност у цьому випадку виглядає так:

rg = n,                       (5.19)

Для нашого випадку маємо таку умову:

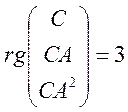
Для нашої моделі ця умова виконується (rg=3), тому система є спостережуваною.

Завдання 5.2 Перевірити на асимптотичну стійкість системи, отримані в завданні 4.5.

Перевірка на стійкість системи

Система (5.42) називається  асимптотично стійкою, якщо для будь-якого x⁰ і будь-якого числа ε > 0 існує таке число N(x⁰, ε), що для розв’язку x(k; x⁰) рівняння (5.42), де x(0; x⁰) = x⁰, виконується x*(k,x⁰)x(k,x⁰) < ε для всіх k>N(x⁰,ε).

Теорема  Для асимптотичної стійкості системи (5.42) необхідно і достатньо, щоб модулі всіх власних чисел матриці А були менше одиниці.

Оскільки усі власні значення по модулю менше одиниці, то наша системае є асимптотично стійкою

Протокол Maple

> with(linalg):

Warning, the protected names norm and trace have been redefined and unprotected

> Q := matrix([[19.79361], [11.29237], [-17.44153], [.572943e-3], [.981240e-3], [-.470211e-3]]);

[ 19.79361  ]

                               [ 11.29237  ]

                               [ -17.44153 ]

                      Q := [.000572943 ]

                               [.000981240 ]

                               [-.000470211]

> A := matrix([[0, 1, 0], [0, 0, 1], [19.79361, 11.29237, -17.44153]]);

                    [   0           1            0    ]

           A := [   0           0            1    ]

                    [19.79361    11.29237    -17.44153]

> B:=matrix([[0],[0],[1]]);

[0]

                            B := [0]

                                    [1]

> C:=matrix([[.572943e-3, .981240e-3, -.470211e-3]]);

C := [.000572943    .000981240    -.000470211]

> AB:=multiply(A,B);

                                [    0    ]

                     AB := [    1    ]

                                [-17.44153]

> AAB:=multiply(A,A,B);

[    1.     ]

                  AAB := [ -17.44153 ]

                                [315.4993387]

> R:=augment(B,AB,AAB);

                      [0        0            1.     ]

             R := [0        1         -17.44153 ]

                      [1    -17.44153    315.4993387]

> Rang := linalg['rank'](R);

                              Rang := 3

> CA:=multiply(C,A);

   CA := [-.009307173152    -.004736853590    .009182439263]

> CAA:=multiply(C,A,A);

   CAA := [.1817536216    .09438432855    -.1648926435]

> P1:=stackmatrix(C,CA,CAA);

            [  .000572943        .000981240       -.000470211 ]

  P1 := [-.009307173152    -.004736853590    .009182439263]

            [ .1817536216       .09438432855     -.1648926435 ]

> Rang2 := linalg['rank'](P1);

                              Rang2 := 3

> Vl := linalg['eigenvals'](A);

            Vl := -.8029240792, 1.368973929, -18.00757985

> Char := linalg['charpoly'](A,`tools/genglobal`[0]('x'));

Char := x0^3+17.44153*x0^2-11.29237*x0-19.79361

X := solve({Char});

X := {x0 = -18.00757985}, {x0 = -.8029240792}, {x0 = 1.368973929}