128 Розділ 4 Обчислення власних значень і власних векторів матриці
Висновки
1. Математична задача обчислення власних значень і векторів матриць набагато складніша, ніж задача розв'язання систем лінійних алгебраїчних рівнянь. Із зростанням розмірності задачі виявляються явні переваги ітераційних методів типу QR-розкладу.
2. Для лінійних моделей об'єктів і систем, заданих системою лінійних рівнянь, власні значення матриці їх коефіцієнтів збігаються з полюсами моделей. Це означає, що не потрібно знаходити передаточні функції й контролювати точність обчислення коефіцієнтів поліномів, їх чисельників і знаменникін і проводити наступне обчислення коренів полінома знаменника. Як відомо, саме через полюси визначаються перехідні процеси в об'єктах, їх смуги пропускання, стійкість та ін., а комплексно-спряжені полюси визначають резонансні явища в поведінці об'єктів.
3. Погана обумовленість лінійних систем рівнянь і жорсткість диференціальних рівнянь визначаються різницею максимального і мінімального власних значень відповідних матриць (коефіцієнтів лінійних рівнянь або перших похідних нелінійних рівнянь). У математичних моделях об'єктів ця різниця визначається конкретними фізичними ефектами і процесами, наприклад ефектом підсилення в електронних схемах, коли сигнали малої потужності на базі транзистора керують сигналами значно більшої потужності на колекторі транзистора. Крім того, причиною вищезгаданих особливостей математичної моделі об'єкта може бути надмірна ідеалізація характеристик його компонентів.
4. Задача обчислення власних значень симетричних матриць виявилася на практиці краще обумовленою порівняно з аналогічною процедурою для несиметричних матриць, оскільки власні значення довільної матриці є більш чутливими до малих змін елементів матриці.
Контрольнізапитаннятазавдання
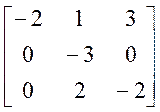
скориставшись методом Крилова, вибрати довільний вектор х = [1, 0,0]T і довести, що система рівнянь (4.10) для коефіцієнтів характеристичного полінома буде ви-родженою.
2 Для матриці
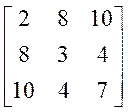
Контрольнізвпитаннятазавдання 129
скориставшись методом Фадєєва-Левер'є, довести, що вектор коефіцієнтів характеристичного полінома b = [1, -12, -139,98]т.
3. Застосуйте метод QR-розкладання для матриці
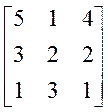
і доведіть, що вектор власних значень матриці λ = [7,509, 0,745 ±і0,4928,0]T .
4. Нехай задано матрицю
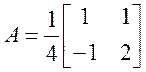
Визначте, чи буде розв'язок системи ![]() асимптотично
стійким, тобто дійсні частини комплексно-спряженнх значень чи самі дійсні
власні значення матриці будуть від'ємними.
асимптотично
стійким, тобто дійсні частини комплексно-спряженнх значень чи самі дійсні
власні значення матриці будуть від'ємними.
5. Безпосередньою підстановкою і застосуванням тригонометричних тотожностей доведіть, що дійсна симетрична матриця порядку пхп
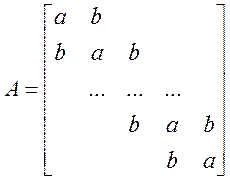
має власні значення λk = а + 2bcos[kπ/(n +1)], k = 1,2,..., п, яким відповідають власні вектори хk = {sin[kπ /(n +1)],..., sin[nkπ/(n +1)]}, k=1,2,..., п.
Покажіть, що для одного QR-розкладання повної матриці А необхідно виконати
4n3/3 операцій. Якщо матриця зведена до форми Хессенбсрга, яка зберігається під час виконання наступних QR-ітерацій, то складність одного QR-розкладання зменшується до 4n2 операцій для несиметричних матриць і до 12n —для симетричних.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.