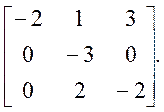
Іn[]:=А={{-2, 1, 3}, {0, -3, 0}, {0, 2, -2}}
0ut= {{-2. 1, 3}, {0, -3, 0}, {0, 2, -2}}
In[]:= CharacteristicPolynomial[A, x]
0ut[]= -12 - 16 х - 7 х2 - х3
In[]:= Simp1ify[-12 - 16 х - 7 х2 - х3]
0ut[]= -(2 + х)2 (3 + х)
Приклад 4.11
Знайти власні значення матриці з прикладу 4.8:
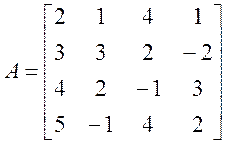
Іn[]:=A={{2, 1, 4, 1}, {3, 3, 2, -2}, {4,2,-1,3}, {5, -1, 4, 2}}
0ut[]= {{2,1,4,1},{3,3,2,-2},{4,2,-1,3},{5,-1,4,2}}
126 Розділ 4.5 Обчислення власних значень матриці в пакеті Mathematica
Іn[]:=Eigenvalues[A]
0ut[]={7.98285, 4.16393, -4.08441, -2.06237},
Матриця А має чотири дійсні власні значення.
Приклад 4.12
Тепер знайдемо власні значення матриці, побудованої після першого кроку перетворення Хаусхолдера у прикладі 4.8. Ця матриця подібна матрииі А, тому їх власні значення повинні збігатися. Дійсно:
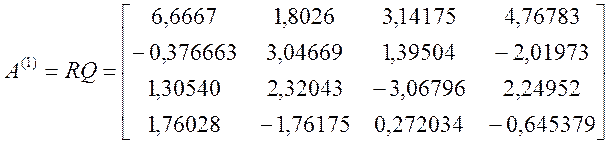
Іn[]:=Al:={{6.6667, 1.8026, 3.14175, 4.76783},
{-0.376663, 3.04669, 1.39504, -2.01973},
{1.30540, 2.32043, -3.06796, 2.24952},
{1.76028, -1.76175, 0.272034, -0.645379}}
Eigenvalues[Al]
0ut[]={7.9829,4.16393,-4.0844,-2.06238}
У пакеті Mathematica реалізовано також QR-алгоритм, що базується на перетворенні Хаусхолдера і викликається стандартним оператором SchurDecomposition[A].
Приклад 4.13
Знайдемо власні значення матриці з прикладу 4.8 і порівняємо їх із результатами, отриманими раніше в прикладі 4.12.
Іn[]:=A:={{2., 1., 4., 1.},
{3., 3., 2., -2.},
{4., 2.,-1., 3.},
{5., -1., 4., 2.}}
{q,r}=SchurDecomposition[A]
0ut[]={{{-0.480124,-0.110723,0.869581,-0.032403},{-0.207422,-0.903897,-0.218297,0.303797},{-0.492336,-0.08314,-0.312533,-0.808094},{-0.695746,0.40472,-0.313845,0.503628}},{{7.98285,1.2333,-3.44342,2.06584},{0.,4.16393,-0.876232,0.58945},{0.,0.,-2.06237,-1.7997},{0.,0.,0.,-4.08441}}}
Іn[]:=MatrixForm[Transpose[r]]
0ut[]=
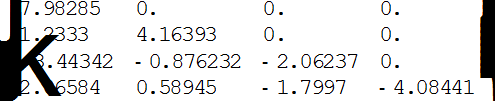
127 Розділ 4 Обчислення власних значень і власних векторів матриці
На діагоналі верхньої трикутної матриці лежать власні значення матриці. Порівнюючи їх і результати прикладів 4.11 і 4.12, можна пересвідчитися, що всі оператори, реалізовані у пакеті, дають однакові результати.
Приклад 4.14
Знайти, користуючись QR-алгоритмом з перетворенням Хаусхолдера, власні значення матриці
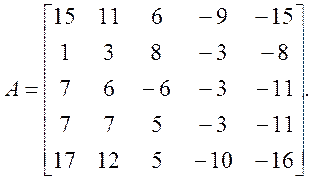
Скористаємося, як і раніше, стандартним оператором SchurDecomposition[A] пакета Mathematica:
Іn[]:=A:={{15., 11., 6., -9.,-15.},
{1., 3., 8., -3., -8.},
{7., 6., -6., -3., -11.},
{7., 7., 5., -3., -11.},
{17., 12., 5., -10., -16}}
{q, r}=SchurDecomposition[A]
0ut[]= {{{0.0929574,0.549951,0.290904,0.191056,0.753515},{-0.396545,0.464417,-0.74449,0.260913,-0.0687687},{0.887067,0.0148288,-0.457883,0.0282837,0.0493443},{0.0101076,0.446266,-0.030579,-0.889828,-0.0895286},{0.217072,0.531506,0.387967,0.320668,-0.645783}},{{-10.6746,1.40927,-3.8738,4.25059,15.2622},{0.,0.22731,-21.4991,12.2005,32.8794},{0.,4.13134,0.22731,4.73529,4.71444},{0.,0.,0.,3.254,2.55549},{0.,0.,0.,0.,-0.034014}}}
Іn[]:= MatrixForm[r]
0ut[]=
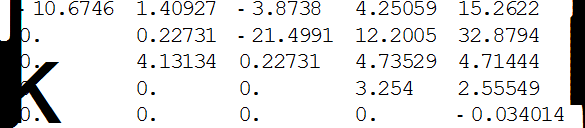
Як бачимо, отримана матриця не є трикутною, ідо свідчить про наявність у матриці А комплексних власних значень. Три дійсні власні значення визначаються діагональними елементами (-10,6746, 3,254, -0,034014), а два комплексні —діагональним блоком другого порядку
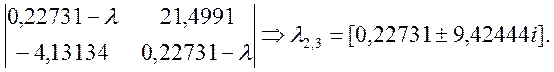
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.