Обчислення власних значень і власних векторів матриці, страница 2

Якщо застосувати степеневий метод до матриці А₂, ітераційний процес бу­де сходитися до наступного за абсолютною величиною власного значення λ₂. Дійсно, якщо рівність (4.32) помножити справа на вектор х_1, отримаємо вираз:

який з огляду на ортогональність власних векторів матриці спрощується і має такий вигляд:

                                                                        (4.33)

    Отже, значення λ=0  і  х = х₁  також є розв'язком рівняння А₂х = λхабо,  інакше кажучи, матриця А₂ має такий набір власних значень: 0, λ₂, λ₃,…, λ_n.  Тобто найбільше власне значення λ₁замінюється значенням 0 й ітерації степене­вого методу будуть збігатися до наступного найбільшого власного значення λ₂. Теоретично можна побудувати потім матрицю А_з і так далі для перебору всіх власних значень. Однак у цьому разі через накопичення похибки результати поступатимуться за точністю і швидкодією результатам, які можна отримати за допомогою QR-алгоритму.

4.4. Власні значення стрічкових матриць

Стрічкову матрицю, яка має три діагоналі, широко використовують під час роз­в'язання диференціальних рівнянь у частинних похідних у разі застосування різницевої апроксимації першої похідної. Наприклад, власні значення матриці

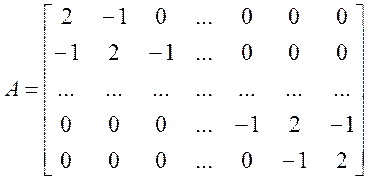
Визначаються виразом

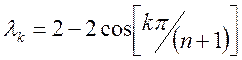                                    ,                                          (4.34)

де  n x n – розмірність матриці.

Доведення формули (4.34) базується на використанні тригонометричної то­тожності

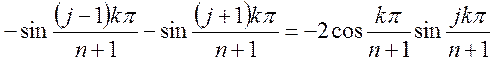,   j,k=1,2,…n.             (4.35)

Якщо до обох частин цього виразу додати член  і потім виписа­ти систему даних виразів, коли j= 1, 2,....n , для фіксованого k,то в матричній формі отримаємо:

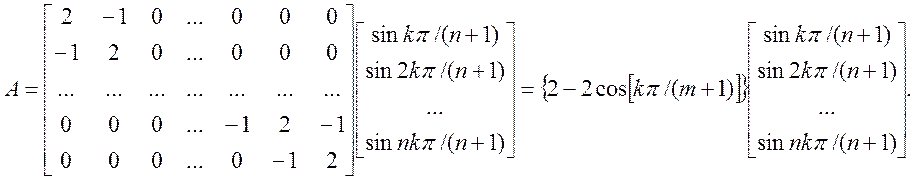                                                                                                (4.36)

За формою цей вираз збігається з (4.1), тому власні значення λ_k  і власні векто­ри будуть дорівнювати:

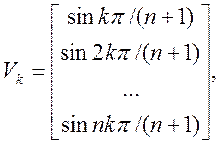      k=1,2,…,n.                (4.37)

Число обумовленості цієї тридіагональної матриці відповідно до виразу (2.62) об­числюється у такий спосіб:

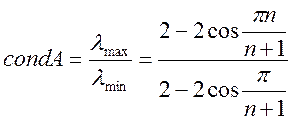                                  (4.38)

Для великих значень п косинуси можна замінити першими членами ряду Тейлора:

                       

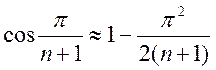
та

                       

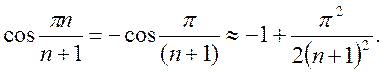
Тому

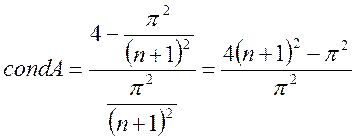                                                           (4.39)

Із формули (4.39) випливає, що тридіагональна матриця А погано обумовле­на і число її обумовленості зростає приблизно як квадрат порядку матриці, що обмежує розмірність сітки під час розв'язування диференціальних рівнянь у час­тинних похідних.

4.5.   Обчисленнявласнихзначеньматриці впакетіMathematica

У пакеті Mathematica реалізовано метод характеристичного рівняння матриці (4.2), який для початкової матриці А запускається такими командами:

♦  Eigenvalues [А] —для обчислення власних значень;

♦  Eigenvectors [А] —для обчислення власних векторів;

♦  Eigensystem  [A]  — для одночасного визначення власних значень і векторів матриці.

При цьому, якщо розмірність становить п<=5, існує аналітичний розв'язок у ра­дикалах, а для обчислень коренів характеристичного рівняння чисельними мето­дами слід замість посилання на матрицю [А] вказати [N[A]]. Ці оператори базу­ються на обчисленні коренів характеристичного рівняння матриці, яке також можливо отримати за допомогою оператора CharacteristicPolynomial[A,х], на­приклад: