Метричні простори
У математиці одним з найбільш фундаментальних понять є поняття границі, а також поняття збіжності. Узагальнення цих понять приводить нас до введення ідеї «відстані».
Нехай маємо деяку множину елементів
однакової природи - ![]() і
і ![]() . Тоді
кажуть, що у множині
. Тоді
кажуть, що у множині ![]() введене поняття метрики або
відстані між елементами . Якщо кожній парі елементів
введене поняття метрики або
відстані між елементами . Якщо кожній парі елементів ![]() ставиться
у відповідність деяке число
ставиться
у відповідність деяке число ![]() , яке обчислюється за
спеціальними правилами і при цьому обов’язково задовольняє трьом аксіомам.
, яке обчислюється за
спеціальними правилами і при цьому обов’язково задовольняє трьом аксіомам.
1) ![]() ;
;
2) ![]() - аксіома симетрії;
- аксіома симетрії;
3) ![]() - аксіома трикутника.
- аксіома трикутника.
Ці аксіоми називаються аксіомами метрики.
Множина елементів ![]() буде називатися
метричним простором, якщо на цій множині введене поняття метрики, яке
задовольняє трьом аксіомам метрики.
буде називатися
метричним простором, якщо на цій множині введене поняття метрики, яке
задовольняє трьом аксіомам метрики.
Фактично, у довільному просторі або множині елементів можна ввести відстань між елементами за різними співвідношеннями головне, щоб вони задовольняли трьом аксіомам метрики. Але для більшості так званих стандартних просторів існує стандартна метрика.
Стандартні простори та їх метрика
1) ![]() - простір дійсних
чисел (множина точок на числовій прямій).
- простір дійсних
чисел (множина точок на числовій прямій).
![]()
2) ![]() - елементи простору –
впорядковані набори з
- елементи простору –
впорядковані набори з ![]() -дійсних
чисел. Фактично
-дійсних
чисел. Фактично ![]() -вимірні
вектори.
-вимірні
вектори.
![]()
![]()
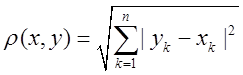
3) ![]()
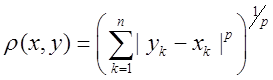
4) ![]() - елементи простору –
нескінченні числові послідовності, ряди з квадратів яких збіжні.
- елементи простору –
нескінченні числові послідовності, ряди з квадратів яких збіжні.
![]()
![]()
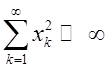
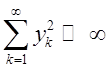
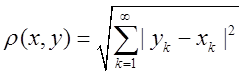
5) ![]()
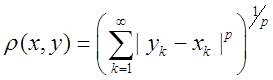
6) ![]() - елементи простору є функції неперервні
на відрізку
- елементи простору є функції неперервні
на відрізку ![]()
![]() -
неперервні функції на
-
неперервні функції на ![]()
![]()
При обчисленні такої відстані приходимо до класичної задачі на знаходження найбільшого значення функції на відрізку, яку розв’язують за допомогою теореми Веєрштрасса.
Але при цьому необхідно не забувати про те, що шукаємо найбільше значення модуля різниці.
7) ![]() - простір функції неперервні на відрізку
- простір функції неперервні на відрізку ![]() разом з усіма своїми похідними до порядку
разом з усіма своїми похідними до порядку
![]() включно
включно
![]()
8) ![]() - елементи простору також неперервні
функції на відрізку
- елементи простору також неперервні
функції на відрізку ![]() , але для них вводиться так звана
інтегральна або середньоквадратична метрика.
, але для них вводиться так звана
інтегральна або середньоквадратична метрика.
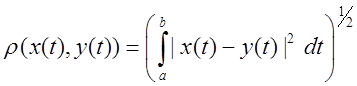
9) ![]()
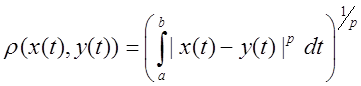
Границя послідовності
Відкриті та замкнуті множини у метричних просторах
Нехай маємо довільний метричний простір ![]() . Тоді відкритою кулею у цьому просторі
називаємо таку множину елементів, яка задовольняє умові:
. Тоді відкритою кулею у цьому просторі
називаємо таку множину елементів, яка задовольняє умові: ![]() ,
, ![]() -
центр кулі,
-
центр кулі, ![]() -
її радіус (задане дійсне число).
-
її радіус (задане дійсне число).
Під поняттям відкритість розуміють строгу нерівність, тобто, елементи, що потрапляють на сферу, яка обмежує кулю не враховуються.
Замкненою кулею називають множину
елементів, яка задовольняє умові: ![]() .
.
Сферою називаємо множину елементів, яка
задовольняє умові: ![]() .
.
Приклади:
1) ![]()
![]()
![]()
![]()
![]()
![]()
2) ![]()
![]()
![]()
![]()
![]()
3) ![]()
![]()
![]()
Нехай маємо метричний простір ![]() і деяку множину елементів
і деяку множину елементів ![]() , таку множину
називають обмеженою, якщо існує така куля
, таку множину
називають обмеженою, якщо існує така куля ![]() , така в
яку можна занурити цю множину, тобто
, така в
яку можна занурити цю множину, тобто ![]() .
.
Під 0 в даному випадку розуміють 0-ий
елемент метричного простору ![]() .
.
Внутрішньою точкою множини ![]() називають будь-яку
точку
називають будь-яку
точку ![]() , яка розташована в цій
множині разом зі своїм
, яка розташована в цій
множині разом зі своїм ![]() -околом.
Таким чином можна сказати, що множина буде відкритою, якщо всі її точки будуть
внутрішніми.
-околом.
Таким чином можна сказати, що множина буде відкритою, якщо всі її точки будуть
внутрішніми.
Наприклад: в просторі ![]() інтервал
інтервал ![]() буде відкритою, а
відрізок
буде відкритою, а
відрізок ![]() буде
замкнутою.
буде
замкнутою.
Можна довести, що будь-яка відкрита куля у метричному просторі завжди буде відкритою множиною.
Границя або межа деякої послідовності є одним з фундаментальних понять математичного аналізу, який має справу тільки з числовими послідовностями. У функціональному аналізі поняття границі послідовності узагальнюється.
Нехай маємо деякий метричний простір ![]() , і маємо послідовність
, і маємо послідовність
![]()
Елемент ![]() буде називатися
границею даної послідовності при
буде називатися
границею даної послідовності при ![]() ,
якщо
,
якщо ![]()
Така збіжність послідовностей
називається збіжністю по метриці даного простору. З геометричної точки зору це
позначає, що будь-який ![]() -окіл точки
-окіл точки ![]() включає в себе всі
елементи послідовності
включає в себе всі
елементи послідовності ![]() за
винятком деякого скінченого їх числа. Факт збіжності послідовності до елемента
за
винятком деякого скінченого їх числа. Факт збіжності послідовності до елемента ![]() означає, що і будь-яка
нескінчена підпослідовність також буде збіжною до елемента
означає, що і будь-яка
нескінчена підпослідовність також буде збіжною до елемента ![]() .
.
Наприклад, для простору ![]() поняття збіжності
послідовності елементів перетворюється на звичайне поняття по координатної
збіжності.
поняття збіжності
послідовності елементів перетворюється на звичайне поняття по координатної
збіжності.
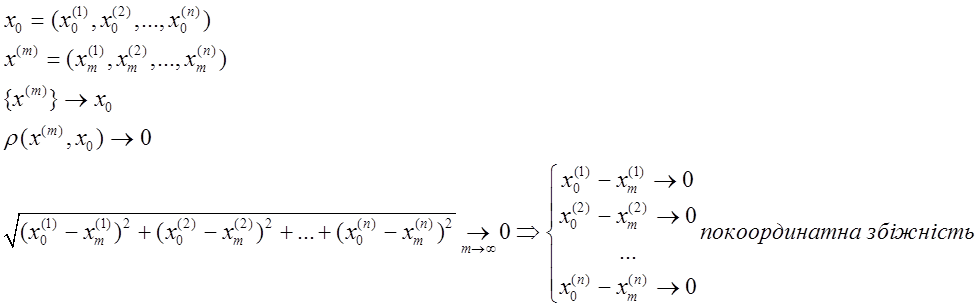 Ця
по координатна збіжність фіксується і в таких просторах як
Ця
по координатна збіжність фіксується і в таких просторах як ![]()
В просторі неперервних функцій ![]() збіжність
послідовності елементів призводить до наступного:
збіжність
послідовності елементів призводить до наступного:
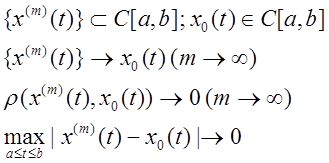
Таку збіжність часто називають рівномірною збіжністю.
Для простору ![]() маємо
наступну збіжність:
маємо
наступну збіжність:
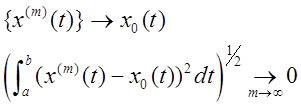
Таку збіжність називають середньоквадратичною збіжністю.
Нехай маємо метричний простір ![]() і деяку множину
і деяку множину ![]() у ньому
у ньому ![]() .
.![]() буде
називатися граничною точкою множини
буде
називатися граничною точкою множини ![]() , якщо в множині
, якщо в множині ![]() знайдеться така послідовність елементів
знайдеться така послідовність елементів ![]() , елементи якої відмінні від
, елементи якої відмінні від ![]() , така, що буде збіжною до точки
, така, що буде збіжною до точки ![]() .
.
![]()
Іншими
словами можна сказати, що у будь-якому околі точки ![]() будуть
існувати точки з множини
будуть
існувати точки з множини ![]() відмінні від
відмінні від ![]() .
.
Якщо множина містить в собі всі свої граничні точки, то вона називається замкненою.
Якщо множина
![]() відкрита,
то після додавання до неї всіх її граничних точок ми отримаємо так зване
замикання множини
відкрита,
то після додавання до неї всіх її граничних точок ми отримаємо так зване
замикання множини ![]() , яке позначаюсь
, яке позначаюсь ![]() . Можна сказати, що замикання множини
. Можна сказати, що замикання множини ![]() -
це найменша замкнена множина, що містить в собі
-
це найменша замкнена множина, що містить в собі ![]() .
.
Теорема.
Нехай ![]() - це відкрита множина у метричному просторі
- це відкрита множина у метричному просторі ![]() ,
тоді доповнення множини
,
тоді доповнення множини ![]() до простору
до простору ![]() позначається
позначається ![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.