Методи побудови функцій належностей нечітких множин: Методичні вказівки до практичного заняття з навчальної дисципліни "Інтелектуальні системи", страница 2

Формальне визначення нечіткої множини не обмежує вибір конкретної функції належності для її подання. На практиці зручніше використовувати ті з них, що дозволяють аналітичне подання у вигляді повної простої математичної функції. Це спрощує не тільки відповідні чисельні розрахунки, але і скорочує обчислювальні ресурси, необхідні для збереження окремих значень функцій належності.

Fuzzy Logic Toolbox містить 11 вбудованих функцій належності, які можна розділити на чотири типи:

·  кусочно-лінійні;

·  гаусівські;

·  сигмоїдні;

·  квадратичні та кубічні.

Для зручності назви всіх вбудованих функцій належності закінчуються на mf.Звернення до функції належності виконується за допомогою такої конструкції:

namemf(x, params),

де  namemf – найменування функції належності;

x– вектор, для координат якого необхідно розрахувати значення функції належності;

params– вектор параметрів функції належності.

Найпростіші функції належності трикутна (trimf) і трапецієвидна (trapmf) формуються з використанням кусочно-лінейної апроксимації. Трапецієвидна функція належності є узагальненням трикутної, вона дозволяє задавати ядро нечіткої множини у вигляді інтервалу. Для трапецієвидної функції належності можлива така зручна інтерпретація: ядро нечіткої множини – оптимістична оцінка; носій нечіткої множини – песимістична оцінка.

Дві функції належності – симетрична гаусівська (gaussmf) та двостороння гаусівська (gaussmf) формується з використанням гаусівського розподілу. Функція gaussmf задає асиметричні функції належності. Узагальнена дзвоноподібна функція належності (gbellmf) по своїй формі похожа на гаусівькі. Ці функції належності часто використовуються в нечітких системах, оскільки на всій області визначення вони є гладкими і приймають ненульові значення.

Функції належності sigmf,dsigmf, psigmf базуються на використанні сигмоїдної кривої. Ці функції дозволяють формувати функції належності, значення яких починаючи з певного значення аргументу і до + (-) дорівнюють 1. Такі функції використовують для завдання лінгвістичних термів типу “високий” або “низький”.

Поліноміальна апроксимація застосовується при формуванні функцій zmf,pimf та smf, графічне подання яких схожі на функції sigmf,dsigmf, psigmf, відповідно.

У Fuzzy Logic Toolbox є можливість для створення власної функції належності. Для цього необхідно сформувати
m-функцію, що містить два вхідних аргументи – вектор, для координат якого необхідно розрахувати значення функції належності і вектор параметрів функції належності. Вихідним аргументом функції має бути вектор ступенів належності. Наприклад,
m-функція, що реалізує дзвоноподібну функцію належності

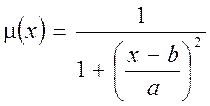
буде містити такий програмний код:

function mu=bellmf(x, params)

%bellmf – bell membership function;

%x – input vector;

%params(1) – concentration coefficient (>0);

%params(2) – coordinate of maximuma.

a=params(1);

b=params(2);

mu=1./(1+ ((x-b)/a).^2);

5 Практичні завдання

Завдання 1: Вивчити 11 вбудованих функцій належностейFuzzy Logic Toolbox. Скласти таблицю, що містить таку інформацію про кожну з них:

1.  Назва функції;

2.  Опис;

3.  Аналітична формула;

4.  Порядок параметрів.

Приклад:

Назва функції	Опис	Аналітична формула	Порядок параметрів
zmf	z-подібна функція належності		[a, b]

Завдання 2: Побудувати графічне зображення типових функцій належності. Порівняти їх з зображеннями, які одержані за допомогою демонстраційного сценарію mfdemo.

Завдання 3: Реалізувати власну функцію належності і побудувати її графічне відображення.