МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
СУМСЬКИЙ ДЕРЖАВНИЙ УНІВЕРСИТЕТ
КАФЕДРА ПРИКЛАДНОЇ І ОБЧИСЛЮВАЛЬНОЇ МАТЕМАТИКИ
ОБОВ’ЯЗКОВЕ ДОМАШНЄ ЗАВДАННЯ
з дисципліни
ФУНКЦІОНАЛЬНИЙ АНАЛІЗ
ВАРІАНТ 21, МОДУЛЬ 3
Виконала: студентка групи ІН-83
Шамшина С. Ю.
Перевірив: Бондар О.В.
Суми, 2010
Задание 1
В
пространстве ![]() суммируемых с квадратом функций рассмотрим
подпространство многочленов степени не выше 2, а в ней - систему элементов
суммируемых с квадратом функций рассмотрим
подпространство многочленов степени не выше 2, а в ней - систему элементов ![]() ,
, ![]() ,
, ![]() .
.
1) Доказать линейную независимость данной системы.
2) Построить
ортонормированную систему ![]() , доказывая
ортогональность построенных элементов на промежуточных этапах.
, доказывая
ортогональность построенных элементов на промежуточных этапах.
3) Аппроксимировать
функцию ![]() элементами данного подпространства.
Найти отклонение
элементами данного подпространства.
Найти отклонение ![]() от найденного элемента.
от найденного элемента.
Решение:
1) Чтобы доказать линейную независимость системы построим определитель Якоби:
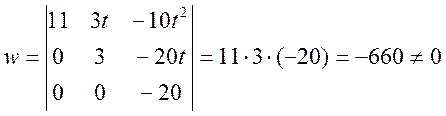
Значит, заданная система является линейно-независимой, и мы можем построить ортонормированный базис.
2) Чтобы построить ортонормированный базис воспользуемся процессом ортогонализации Шмидта.
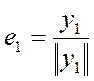
![]()
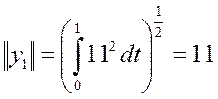
![]()
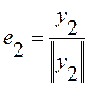
![]()
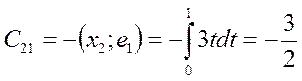
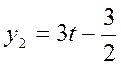
![]()
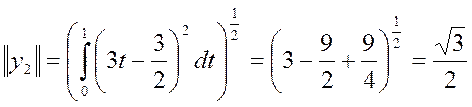
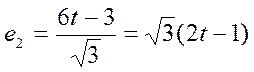
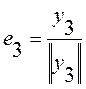
![]()
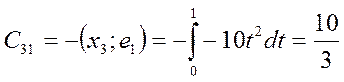
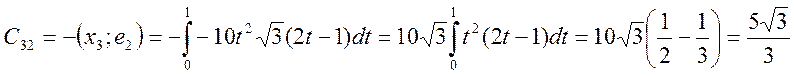
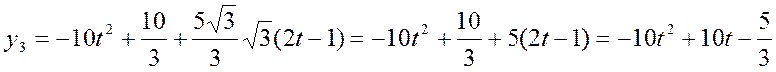
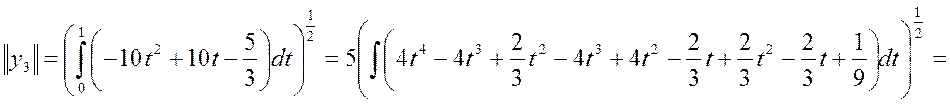
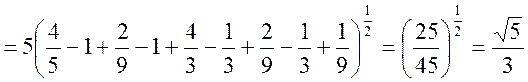
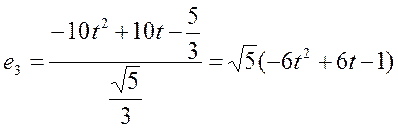
Проверка базиса:
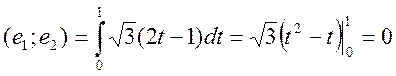
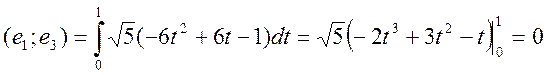
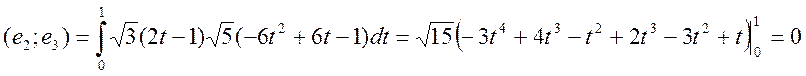
Значит, ортонормированная система построена правильно.
3) Аппроксимация:
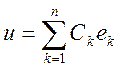
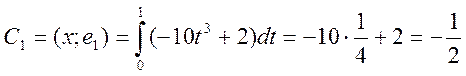
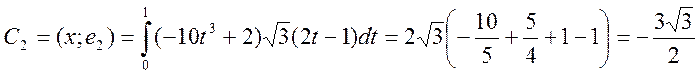
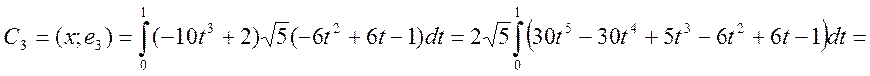
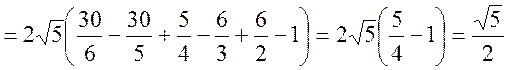
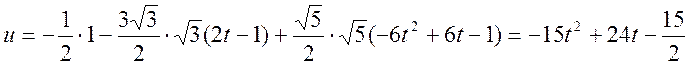
Отклонение:
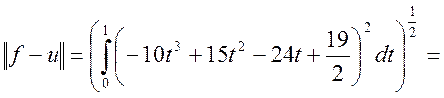
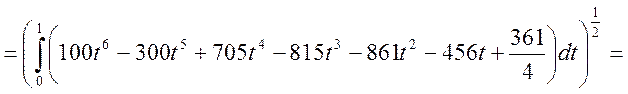
![]()
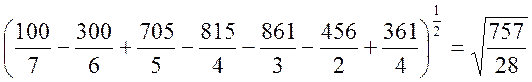
Задание 2
В пространстве R3 задана
система элементов ![]() .
.
(3,-1,1), (5,-1,2), (1,2,4)
1) Доказать линейную независимость данной системы.
2) Построить ортонормированную
систему ![]() , доказывая ортогональность построенных
элементов на промежуточных этапах.
, доказывая ортогональность построенных
элементов на промежуточных этапах.
Решение:
1) Докажем линейную независимость системы используя определитель Грамма.
![]()
![]()
![]()
![]()
![]()
![]()
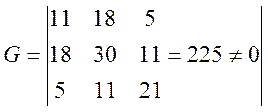
Определитель Грамма не равен нулю, значит система линейно-независимая.
2) Построим ортонормированный базис:
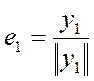
![]()
![]()
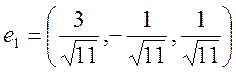
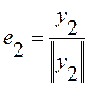
![]()
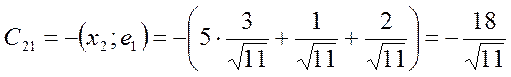
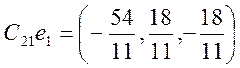
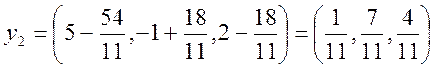
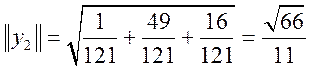
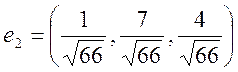
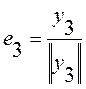
![]()
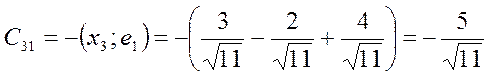
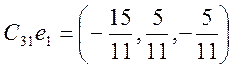
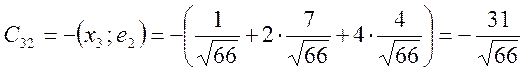
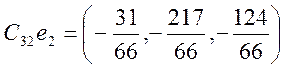
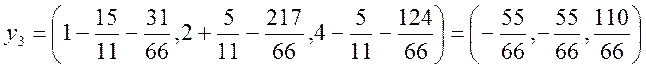
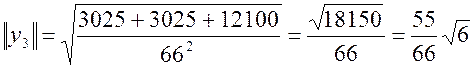
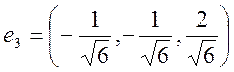
Проверка:
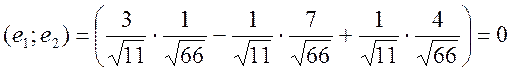
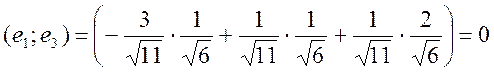
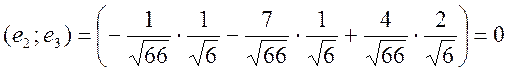
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.