







МІНІСТЕРСТВО ОСВІТИ І НАУКИ УКРАЇНИ
СУМСЬКИЙ ДЕРЖАВНИЙ УНІВЕРСИТЕТ
ОБОВ’ЯЗКОВЕ ДОМАШНЄ ЗАВДАННЯ
з дисципліни
МАТЕМАТИЧНА СТАТИСТИКА
МОДУЛЬ 2
ВАРІАНТ 19
Виконав: студент групи ІН-83
Чирва А.С.
Перевірив: проф. Мазманішвілі А.С.
Суми, 2010
Задача №1
Отримана
вибірка об’єму ![]() :
:
7,
1, 4+m, 3, 2+k, 16+2![]() , 15+n,
4, 1, 1, 3+k, 5,
, 15+n,
4, 1, 1, 3+k, 5,
5, 6, 6, 6, 1, 5+m, 3+n, 14+2m, 2, 2, 7, 7, 7, 4, 4,
3, 1, 2+p, 6, 8, 4, 15+3p, 1+k, 1+m, 1+n, 5, 5, 3.
k = 2, m = 3, n = 1, p = 4.
В задачі потрібно:
1. Побудувати: інтервальний варіаційний ряд розподілу; гістограму; емпіричну функцію розподілу.
2. Знайти: вибіркове середнє, вибіркову дисперсію, середнє квадратичне відхилення, медіану і моду вибірки.
3. Оформити результати графічно.
Розв’язання
Вибірка
{7,1,7,3,4,16,18,4,1,1,5,5,5,6,6,6,1,8,4,20,2,2,7,7,7,4,4,3,1,6,6,8,4,27,3,4,2,5,5,3}
Відсортована вибірка за зростанням
{1,1,1,1,1,2,2,2,3,3,3,3,4,4,4,4,4,4,4,5,5,5,5,5,6,6,6,6,6,7,7,7,7,7,8,8,16,18,20,27}
1. Щоб побудувати інтервальний варіаційний ряд розподілу, ми використовуємо згруповані статистичні ряди наступного виду:
|
Значення |
1 |
2 |
3 |
4 |
5 |
6 |
|
Частота |
5 |
3 |
4 |
7 |
5 |
5 |
|
7 |
8 |
16 |
18 |
20 |
27 |
|
5 |
2 |
1 |
1 |
1 |
1 |
Обчислюємо крок розбиття інтервалу вибірки на під інтервали:
![]()
![]()
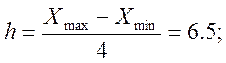
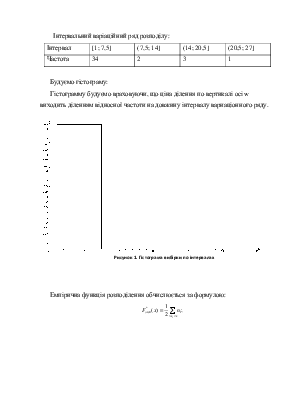
Інтервальний варіаційний ряд розподілу:
|
Інтервал |
[1; 7,5] |
(7,5; 14] |
(14; 20,5] |
(20,5; 27] |
|
Частота |
34 |
2 |
3 |
1 |
Будуємо гістограму:
Гістограмму будуємо враховуючи, що ціна ділення по вертикалі осі w виходить діленням відносної частоти на довжину інтервалу вариаціонного ряду.
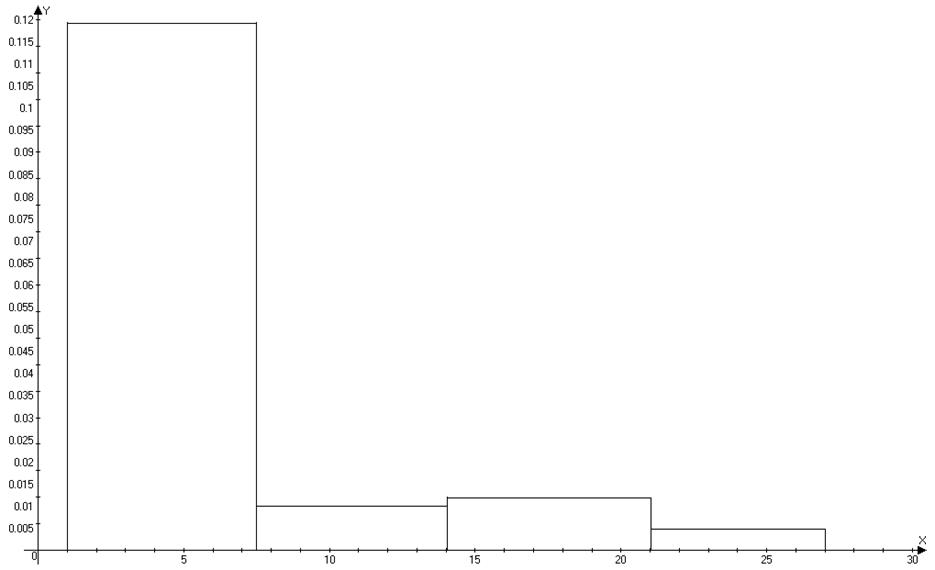
Рисунок 1. Гістограма вибірки по інтервалах
Емпірична функція розподілення обчислюється за формулою:
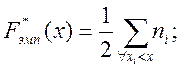
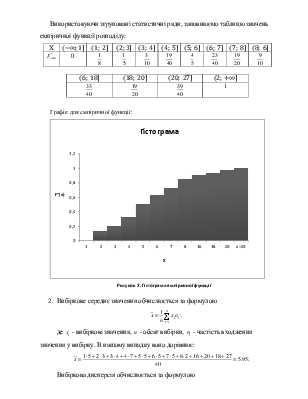
Використовуючи згруповані статистичні ряди, заповнюємо таблицю значень емпіричної функції розподілу:
|
Х |
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
Графік для емпіричної функції:
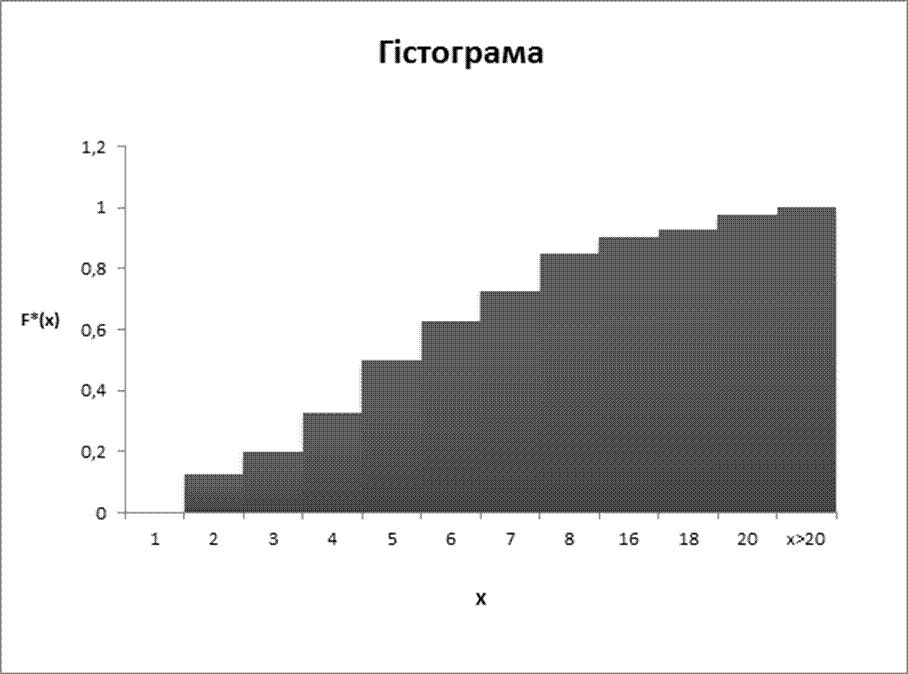
Рисунок 2. Гістограма емпіричної функції
2. Вибіркове середнє значення обчислюється за формулою
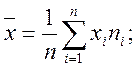
де ![]() -
вибіркові значення,
-
вибіркові значення, ![]() - обсяг вибірки,
- обсяг вибірки, ![]() -
частість входження значення у вибірку. В нашому випадку воно дорівнює:
-
частість входження значення у вибірку. В нашому випадку воно дорівнює:
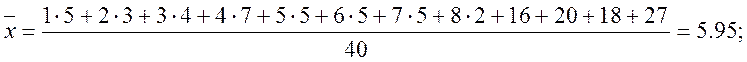
Вибіркова дисперсія обчислюється за формулою
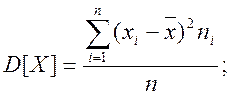
де
![]() - вибіркові значення,
- вибіркові значення, ![]() - вибіркове середнє,
- вибіркове середнє, ![]() - обсяг вибірки. В нашому випадку вона
дорівнює:
- обсяг вибірки. В нашому випадку вона
дорівнює:
![]()
Середнє квадратичне відхилення знайдемо за формулою:
![]() ,
,
де
![]() - вибіркова дисперсія. В нашому випадку
воно дорівнює:
- вибіркова дисперсія. В нашому випадку
воно дорівнює:
![]()
Так як кількість наших спостережень парна, то медіана вибірки обчислюється за формулою:
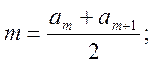
де
індекс при ![]()
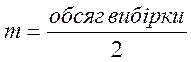 . В нашому випадку
медіана дорівнює:
. В нашому випадку
медіана дорівнює:
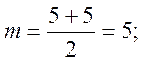
Задача № 2
Випадкова величина Х задана густиною розподілу ймовірностей:
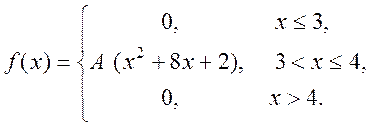
Знайти: параметр A; функцію розподілу F(x); математичне сподівання M[X]; дисперсію D[X]; ймовірність P(π/4≤X≤π). Роботу оформити графічно.
Розв’язання
Параметр А:
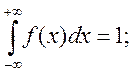
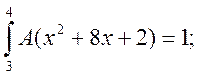
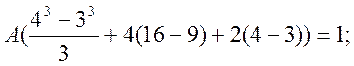
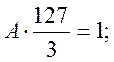
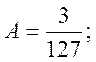
Функція розподілу:
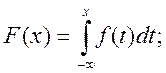
Нехай ![]() , тоді
, тоді
![]()
Нехай ![]() , тоді
, тоді
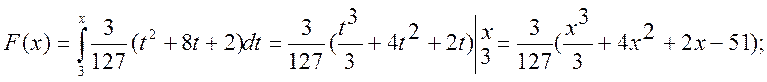
Нехай ![]() , тоді
, тоді
![]()
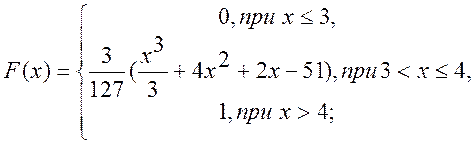
Математичне сподівання:
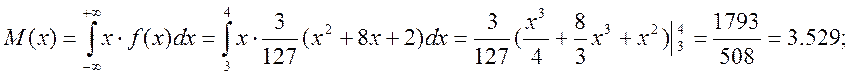
Дисперсія:
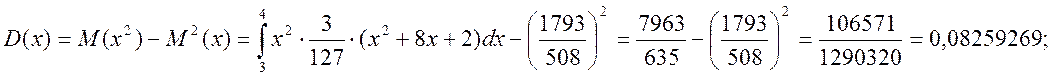
Ймовірність
![]()
В термінах інтегральної функції розподілу маємо,
![]()
тобто
ймовірність потрапляння результату спостережень, або випадкової похибки в
заданий інтервал дорівнює різниці значень функції розподілу на границях цього
інтервалу. Підставивши, наші значення ![]() у
функцію розподілу,
у
функцію розподілу,
отримаємо
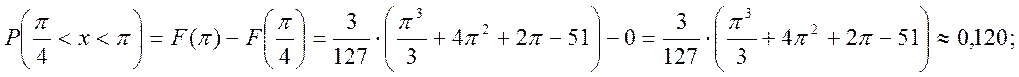
Задача № 3
Густина розподілу випадкової величини X задана формулою
![]() ,
,
якщо ![]() , та нулю в протилежному випадку.
, та нулю в протилежному випадку.
Знайти:
Cталу A, функцію
розподілу ![]() . Визначити значення ймовірностей
. Визначити значення ймовірностей
Pr{![]() >0.5} та Pr{0,25<X<0.5}.
>0.5} та Pr{0,25<X<0.5}.
Розв’язання
Параметр А:
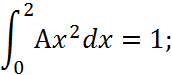
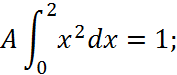
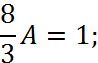
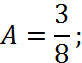
Функція розподілу:
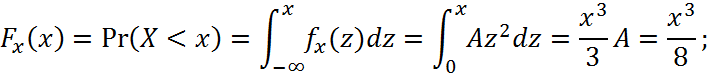
Ймовірність Pr(0.25≤X≤0.5).
В термінах інтегральної функції розподілу маємо,
![]()
![]() 0.015625-0.001953125
= 0,013671875;
0.015625-0.001953125
= 0,013671875;
Ймовірність Pr{![]() >0.5}
>0.5}
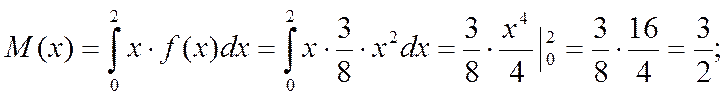
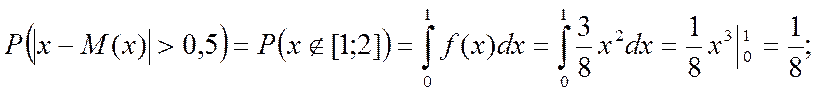
Задача № 4
Випадкова величина X рівномірно
розподілена на інтервалі [-1,1]. Відомо, що Y=X![]() .
.
Приймаючи, що цілочисельний параметр m>0 є заданим, знайти коефіцієнт кореляції між випадковими величинами X і Y
Розв’язання
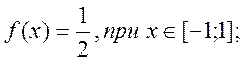
Оскільки
величина Х рівномірно розподілена на інтервалі [-1,1], то математичне
сподівання ![]() знаходимо за
формулою:
знаходимо за
формулою:

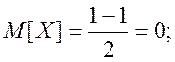
Оскільки
величини Y
та
Х, зв’язані за законом Y=X![]() , то математичне сподівання
, то математичне сподівання ![]() знаходимо за формулою:
знаходимо за формулою:
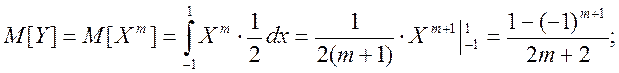
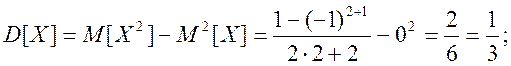
Дисперсія
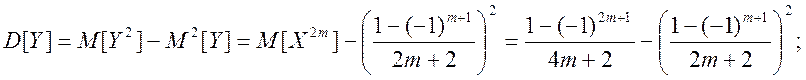
Коефіцієнт корелції:
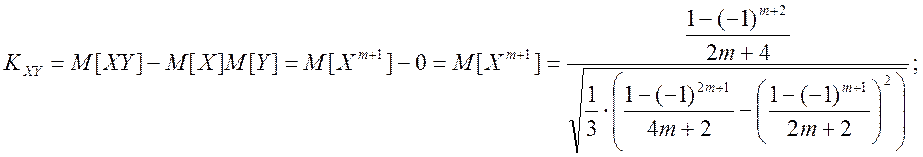 .
.
Задача № 5
Випадкова
величина X має густину розподілу ймовірностей ![]() ,
, ![]() ; незалежна від неї випадкова величина Y
має такий же закон розподілу.
; незалежна від неї випадкова величина Y
має такий же закон розподілу.
Знайти
густину розподілу відношення 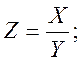 .
.
Розв’язання
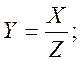
Функцію розподілу густини знайдемо за формулою:
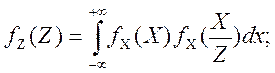
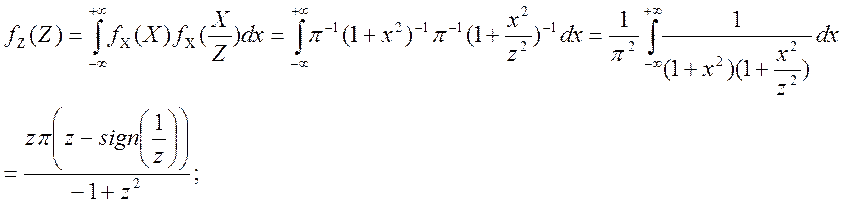
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.