




Практична робота №3.2
Багатошаровий перцептрон
1. Побудова нейронних мереж в середовищі MATLAB.
2. Дослідження можливостей розпізнавання друкованих символів за допомогою нейронних мереж.
3. Розпізнавання друкованих символів за допомогою навченої нейронних мереж.
Багатошарові перцептрони можна побудувати каскадним поєднанням одношарових перцептронів. Вони здатні виконувати більш загальні класифікації. Відділяючи точки, що знаходяться у випуклих або необмежених областях.
Було доведено, що завжди можна обійтися одним прихованим шаром із достатньою кількістю нейронів. Збільшення прихованого шару збільшує розмірність простору, в якому проводиться класифікація.
Багатошарові перцептрони досить популярні в нейроінформатиці, що обумовлено занчною кількістю задач,які можна розв’язувати з їх допомогою. Серед них класифікація, кластеризація, розпізнавання образів, фільтрація, тощо.
Існує значна кількість алгоритмів навчання багатошарових перцептронів. В основному вони поділяються на дві категорії:
- градієнтні алгоритми,
- стохастичні алгоритми.
До першої групи належать ті, що базуються на обчисленні похідної функції помилки та корегуванні вагових коефіцієнтів у відповідності зі значенням знайденої похідної. кожен наступний крок направлений в сторону антиградієнта функції помилки. Основу цих алгоритмів складає алгоритм зворотного розповсюдження помилки.
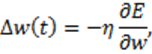
де функція помилки
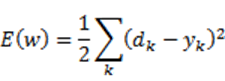
На сьогодні існує багато модифікацій цього алгоритму, які дозволяють значно підвищити його ефективність. Найбільш відомими з них є:
1. Навчання з моментом. Ідея методу полягає в додаванні до корекції вагового коефіцієнту значення пропорційного розміру попередньої зміни цього ж вагового коефіцієнту
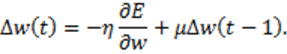
2. Автономний градієнтний алгоритм – навчання з автоматичною зміною довжини кроку.
3. PPROP – алгоритм, у якому кожний ваговий коефіцієнт має свій темп навчання.
Стохастичні методи навчання використовують псевдовипадкові зміни величин вагових коефіцієнтів, запам’ятовуючи такі зміни,що ведуть до поліпшення характеристик мережі. До цієї групи алгоритмів належать такі алгоритми:
1. Алгоритм пошуку у випадковому напрямку.
2. Больцманівське навчання.
3. Навчання Коші як доповнення до Больцманівського навчання.
Основним недоліком цієї групи алгоритмів є велика кількість часу, потрібного на навчання, а відповідно і великі числові затрати. В той же час, ці алгоритми забезпечують глобальну оптимізацію, тоді як градієнтні методи в більшості випадків дозволяють знайти лише локальні мінімуми функціоналу помилки.
Навчальна матриця складається для M=10 класів розпізнавання. Навчання буде проводитися лише за еталонним, таким чином навчання буде проводитися лише за однією реалізацією для кожного класу.
Кожний еталон подамо в графічному вигляді в бітовому форматі. Тип файлу визначається типами графічних файлів, що використовуються в середовищі MATLAB. Наприклад, bmp або tif.
Для формування графічних файлів образів можна застосувати “Adobe Photoshop”. При цьому необхідно виконати таку послідовність операцій:
1) створити новий файл з параметрами:
- - ім’я : XXXX;
- - ширина: N1 пікселів;
- - висота: N2 пікселів;
- - кольоровий режим: бітовий формат.
Значення N1, N2=8…20 задаються викладачем.
2) за допомогою інструментів типу «Кисть», «Ластик» сформувати образи символів.
3) зберегти файл.
На рис. 1 наведено приклади графічних символів цифр при N1=10, N2=12 пікс.










Рис. 1 – Приклад графічних символів цифр
На даному етапі в середовищі MATLAB виконується:
- формування числових масивів еталонних образів;
- підготовка даних, необхідних для створення нейронної мережі;
- створення ШНМ, завдання параметрів навчання нейронної мережі та її навчання.
формування числових масивів еталонних образів
Еталонний образ кожного символу подано у вигляді вектору-стовпця [N,1], число елементів N в якому відповідає числу ознак. Такий вектор-стовпець формується з двовимірного масиву-зображення [N1,N2], який формується при зчитуванні графічного файлу образа за допомогою команд:
imread (FILENAME) - процедура зчитування графічного файлу;
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.