Специфика использования библиотеки mmath на примере проверки простоты больших чисел

ЛЕКЦИЯ №2. 28.02

Специфика использования библиотеки mmath на примере проверки простоты больших чисел.

r – сдвиг на слово.

r _b – сдвиг на биты

mmath.h

int Rabin(P, int k);

m_long y;

m_shl (s, rb)

r=(r<<5)+rb

P-1=2r*S

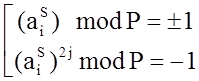
for (i=0; i<k; i++) {

m_rand (x, P[0]-1);

m_blockpowmod(x,S,P,y);

if(m_cmp(y,P-1)||(y[0]!=1))

for(int y=1; j<r, j++){

m_sqr(y, y);

m_div(y,P,m,y)

if (m_cmp==0) break;}

if (j=r) return 1;}

int DivTest(m_long P, int b)

P[0]=Q[0]=32;

{

m_rand (P, P[0]); P[1]!=1;

while (DivTest(P, P[0])||Rabin (P,60));

}

Вариант реализации теста Рабина-Миллера для массива простых чисел от 0 до 65519.

#include <merror.h>

#include <MMATH.h>

#include <MDEF.h>

#include <DivTest.h>

#include <iostream.h>

#define PRIME_2BYTE (6542) // количество двухбайтовых простых чисел

#define PRIME_1BYTE (54)

#pragma hdrstop

int Rabin(M_LONG P, int toc);

int DivTest(M_LONG P,unsigned char num);

#pragma argsused

int main(int argc, char* argv[])

{   int non;

unsigned long Prime[]={2L,3L,5L,7L,11L,13L,17L,19L,23L,29L,31L,

37L,41L,43L,47L,53L,59L,61L,67L,71L,73L, 79L,83L,89L,97L,101L,103L, 107L,109L,113L,127L, 131L,137L,139L,………………………………………..

………………………………………………………………………….. ,65519L,

65521L};

srand(time(NULL));

M_LONG       P={1,24313};

if(DivTest(P,100))

return 1;

 non=Rabin(P,60);

 cout<<non;

  cin>>non;

        return 0;

}

 int Rabin(M_LONG P, int toc){

 M_LONG  P_1, a, temp, s, temp1,temp2, temp3, temp4;

 M_LONG one={1,1};

   int y=0, rb=0, t, t1=0;

   m_copy(P_1,P);

 P_1[1]&=0xFFFFFFFE;

  for (unsigned int i=1;i<=P_1[0];i++){

        if(P_1[i]==0)

         y++;

        else break;}

        temp[0]=P_1[0]-y;

        for (int j=1; j<=temp[0];j++)

        temp[j]=P_1[y+j];

        for (unsigned long mask=1;(temp[1]&mask)==0;){

        mask=mask<<1;

        rb++;}

        t=y*32+rb;

   m_shr(temp,t);

   int j=0;

   for (int k=0;k<toc;k++){

   m_rand(a,P[0]);

   m_blockmontpowmod(a,temp,P,temp1);

   if ((m_cmp(temp1,one))*(m_cmp(temp1,P_1))!=0){

       for (j=1;j<t;j++){

        m_sqr(temp1,temp2);

        m_div(temp2, P, temp3, temp1);

        if (m_cmp(temp1,P_1)==0)

                break;}

        if (j==t)

        return 1;

        }      }

     return 0; }

     int DivTest(M_LONG P,unsigned char num){

            register int i;

            M_LONG q;

            DIGIT rem;

            num=(num==2)?PRIME_2BYTE:PRIME_1BYTE;

            for(i=0;i<num;i++){

                        m_div1(P,Prime[i],q,&rem);//rem-остаток

                        if(rem==0)// делится нацело

                                    return 1;

                        if(P[0]==1 && P[1]<=Prime[i])

                                    return 0;}

            return 0;}

ЛЕКЦИЯ 3. 3.03

Реализация простейших арифметических операций для целочисленного деления

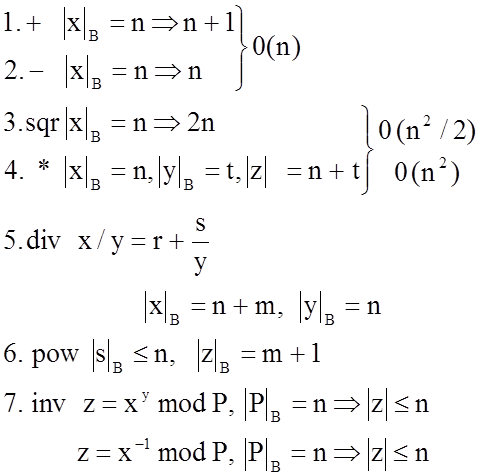
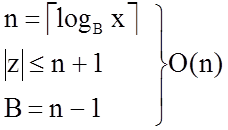
X=(x₁…x_n)_B

Y=(y₁…y_k)_B

Z=(z₁…z_m)_B

for (i=0; c=0; i<n; i++){

r_i=(x_i-y_i+c+B) mod B;

c=[(x_i-y_i+c+B)/B]

}

1. Метод умножения со сканированием операнда

2. Метод умножения со сканированием произведения.

B=2^w

X=(x_n …x_2, x₁)_B

Y=(y_t…y₂, y₁)_B

Z=(z_n+t…z₂, z₁)_B

For (i=1; i<=n+t; i++) z_i=0 //обнуляем

     For (i=1; i<=n; i++) {      //по x_i

     u=0;

            for (j=1; j<t; j++){    //по y_i

(u,v)_B ← Z_i+j-1+x_i*y_i+г

//операция внутреннего произведения

Z_i+j-1=V

//

Z_i+j-1=u;

}  //for ;

Пример:

b=10, n=2, t=3

n+t=5;

x=(89)_b

y=(769)_b

i	j	u	Zi+j-1+xiyi+u	Z5	Z4	Z3	Z2	Z1	u*v
1	1	0	0+9*9+0	0	0	0	0	1	81
	2	8	0+9*6+8=62	0	0	0	2	1	62
	3	6	0+9*7+6=69	0	6	9	2	1	69
2	1	0	2+8*9+0=74	0	6	9	4	1	72
	2	7	9+8*6+7=64	0	6	4	4	1	64
	3	6	6+8*7+6=68	6	8	4	4	1	68

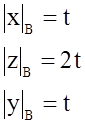
(r₂ r₁ r₀)_B←(0,0,0)

for (k=1; k<2t; k++){

(i,j)/i+j=k;   0≤i,j≤t}

(u,v) ←x_i y_i

(c₁ r₀)←r₀ w //бит переноса

(c₁ r₁)←r_i+u+c //бит с учетом переноса
r₂=r₂+c

r_k=r₀, r₀=r₁, r₁=r₂, r₂=0

r_2t=r₀

 

Метод Карацубы

56           56

224                                                                                 224

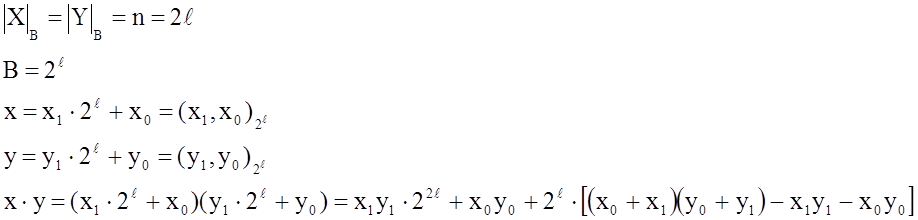
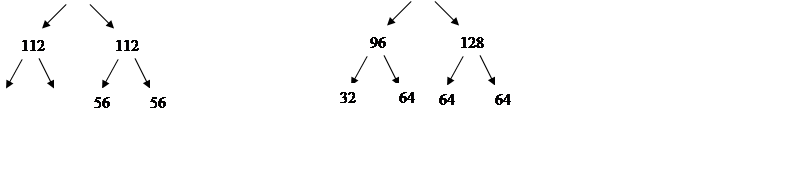                                                                                                                      9 “*” по 64

                                                                                                                       3“*” по 32

                        12 “*” 64 бита

|X|_B=t

|Z|=2t

for (i=1; i<=2t; i++) z=0

for (i=1; i<=t; i++){(u v)_B←r_ℓi-1+x_i²

z_2i-1=v, c=u

for (j=i+1; j<=t; j++){

(u v)_B←r_i+j-1+2x : y_i+c_i

z_i+j-1=v, c=u

            z_i+t-1=u

t²+t/2

}}

ЛЕКЦИЯ 4. 3.03

Изучение специфики представления функций библиотеки miracl

1. Арифметика больших целых чисел Big
2. Арифметика больших дробных чисел Flash
3. Арифметика ЭК E(Fp)

     E(F₂^m)

4. AES.
5. SHA – 160 бит.

  X[1]