Специфика использования библиотеки mmath на примере проверки простоты больших чисел, страница 2

s

m

n

lsv

msw

msw

                                                                                                                                   X[n+m]

s - знаковый бит

n – длина числителя, целого числа

m – длина знаменателя

0=2³² – max

функция выделения памяти

miracl * mirsys(int len, int Base);

                  base – основание системы счисления

Если len=10 а base=16, то выделяется 10*16 бит

Return: указатель типа (miracl *)

функция освобождения памяти

void mirexit();

функция выделения памяти под переменную типа big или flash

flash mirvar (int I^V)

I^V – записывает в созданную big, flash

процедура высвобождения памяти из-под переменной

mirkill(big x) void

Пример

Extern “c”{

#include “miracl.h”

}

miracl *mip=mirsys(100,0);

big n1, n2, flash 3;

n1=mirvar(1);

n2=mirvar(2);

…………….

mirkill(n1);

mirkill n2);

mirexit();

Функции:

1.  ввода-вывода;

2.  преобразования типов

3.  генерация n случайных чисел

4.  арифметические и логические операции низкого уровня

int innum(flash x, file*f);

int instr(flash x, char*str);

int cinstr(flash x, char*str);

2≤(mip->iobase)=256;

 big x=mirvar(1);

instr (x, “fffff….”);

int otnum(flash x, file*f);

int cotnum(flash x, file*f);

int otstr (flash x, char*str);

int cotstr (flash x, char*str);

void bytes_to_big (int len, char * bytes, big x);

void big_to_bytes(int max, big x, char *bytes);

void convert(int n, big x);

void lpconv(long n, big x);

int compare(big x, big y)

-1: x<y

1: x>y

0:x=0;

int getdipit(big x, int i);

void putdip(int n, big x, int i);

определение количества цифр в числе

int numdig  (big x),

функции копирования

void copy(flash x, flash y);

void zero(flash x);

функция изменения макс. числа

определение знака

int exsiqh(flash x)//±1

void insiqh(int s, flash x);

void irand(long seed);

int brand();

int brand(big max, big x);

1<x<max

void strong_init(int len_seed, char *seed, long tod);

void strong_rng(int len_byte, char *x);

void strog_bigrand(big max, big x)

1<x<max

ЛЕКЦИЯ 5. 7.03

Изучение вариантов реализации редукции для целых чисел (классический метод, метод Баретта)

Классический метод

X^k (mod P)

t+1

                                                                                                                                                                                                                                                                                

b=(2^w_n=32)

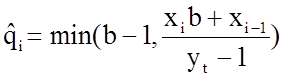
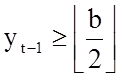
y*d

x*d                  d-коэффициент

d=2^k

 

 

Метод Баретта

   

                

         

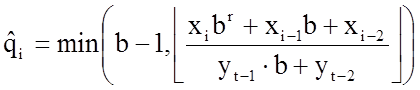
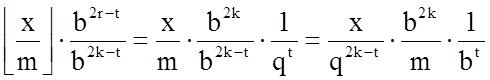
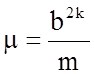
1.                    

2.        (=r₁-r₂)

3. if

4. while       // max 2 page

Численный пример

b=4 (любое b>3)

m=(233)₄=(47)₁₀; k=3

x=(313221)₄         

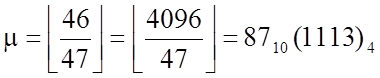
1.1.

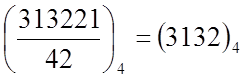
1.2. (3132)₄*(1113)₄=(10231302)₄

1.3. 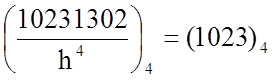     (при делении сдвиг вправо на k+1)

2.1. (313221)₄mod4⁴=(3221)₄r_i

2.2. (1023)₄*(233)₄mod4⁴=(313011)₄mod4⁴=(3011)₄

2.3. (3221)₄-(3011)₄=(210)₄=(36)₁₀

I=(k²+5k+2)/2

k – разрядность модуля. Оценка сложности

2⁶⁴+2³²                      01100000
ЛЕКЦИЯ №6. 9.03

Простейшие методы и алгоритмы возведения в степень: бинарный и блочный метод.

Метод возведения в степень справа налево

x^R mod P, R=23₁₀=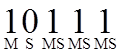    M-умножение, S-возведение в квадрат

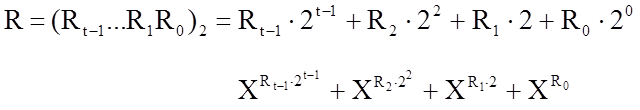
Алгоритм

M=1; S=x

for (i0, i<t, i++)

{ if (R_i==1)

M=(M*S) mod P

S=(S*S) mod P }

Пример

R=23₁₀     x – число большой разрядности

M	1	x	x3	x7	-	x23
R	(10111)	1011	101	10	1	0
S	x

I+wt(R)

Метод возведение в степень слева направо

			Старший бит 1 – отбрасывается, если 0 – возводим в квадрат, если 1 – возв. в квадрат и умножаем

 

1

23₁₀=                            

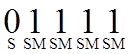
Алгоритм:

M=x

for (i=t-2, i>=0, i--)

{ M=M² mod P

   if (R_i==1) M=(M*x) mod P }

i	-	3	2	1	0
Ri	-	0	1	1	1
M	x	x2	x4 x5	x10 x11	x22 x23

I+wt(R)-1

Блочный метод (метод окна)

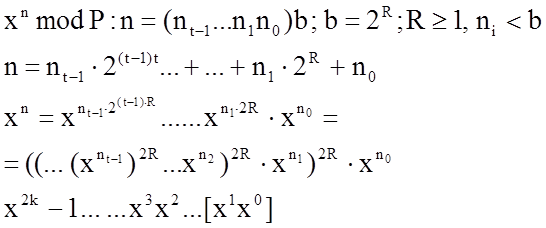
Алгоритм:

X[0]=1; X[1]=x

For(i=1; i<=2^R-1; i++)

X[i]=X[i-1]*x

M=1;

For (i=t-1; i>=0; i--)

{M=M^2R mod P

M=M*X[n_i] mod P}

I+I_M*I_S

 

Пример

n=23₁₀=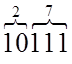=(n₁*n₀)=(27)₈          R=3  (Перевод в 8-ричную систему счисления)

i	-	1	0
ni	-	2	7
M	1	1*x2	(x2)8=x16; x16*X[7]=x23

Модифицированный блочный метод

X[0]=1; X[1]=x; X[2]=x²

For(i=1; i<=2^R-1; i++)

X[2_i+1]=X[2_i-1]*X[2];

M=1;

For (i=t-1; i>=0; i--)

{}

Метод скользящего окна

//Предвычисления (см. метод. выше)

                                    (n_t+1….. n₂ n₁ n₀)₂

M=1; i=t-1;

While (i>=0)

{ if (n_i==0) {M=M² mod P;

         i--;} else{ n_in_i-1… n_l) //выделение подстроки, так, что

i-l+1<=R и n_l=1

;

i=l-1; }

}