Специализированные методы редукции для фиксированных триномов и пентаномов

14 Специализированные методы редукции для фиксированных триномов и пентаномов

Алгоритм               Пословная редукция (метод Шроппеля) для

f  (x) = x¹⁶³ + x⁷ + x⁶ + x³ + 1.

¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾

ВХОД:            , определяемое фиксированным триномом или пентаномом f (x) = (f _m ‑ 1 … f ₁ f ₀ ) ₂ = (f _L … f ₂ f ₁ ) ,

                        s (x) = (s _2×m – 1 … s ₁ s ₀ ) ₂ = (s _n … s ₂ s ₁ ) (т.е. deg(s (x)) = 2×m > m ) ;

                        w ¾ размер слова (w = 32).

ВЫХОД:         s (x) = s (x) mod f (x), s (x) = (s _m – 2 … s ₁ s ₀ ) ₂

                        (deg(s (x)) = m ‑ 1 = < m).

¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾¾

1.    for ( i = n; i > L ; i - -) { // по словам s от старших к младшим

               1.1    T = s _i ;

               1.2    s _i - 6 ^ = T << 29;                                          // 6 - тое слово при i = 12 

               1.3    s _i - 5 ^ = (T<<4)^(T<<3)^T^(T>>3);            // 7 - ое слово при i = 12 

               1.4    s _i – 4 ^ = (T>>28)^(T>>29);                         // 8 - ое слово при i = 12 

       }

2.    T = s ₆ & 0xfffffff8 ; // Очистка бит 0, 1, 2 значения s ₆ 

3.    s ₁ ^ = (T<<4)^(T<<3)^T^(T>>3);

4.    s ₂ ^ = (T>>28)^(T>>29);

5.    s ₆ & = 0x00000007;       // очистка верхних неиспользуемых бит значения s ₆ ( ≥ 163)

                                               // 6 слово: 160 ÷ 191

6.    коррекция длины s (x); // if(s[0] > f[0]) s[0] = f[0];

M_LONG f= {6, 0xC9, 0, 0, 0, 0, 0x8};

12 сл. 352 ¸ 383 бита

1. g(x)= x³⁵²Å  f(x)
2. g(x) = x393 Å f(x)

g(x)= x ^m1 (m₁³ m)

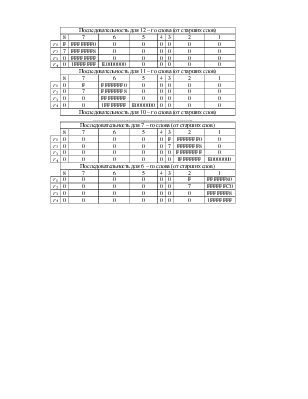
Приклад розрахованих попередніх таблиць для формування констант алгоритму пословної редукції (метод Шроппеля) для модулю f(x) = x ¹⁶³ + x ⁷ + x ⁶ + x ³ + 1 (№ 1 із ДСТУ 4145 ‑ 2002)