







ЛЕКЦІЯ 3
Використання модульної арифметики. Обчислення з многочленами. Методи множення. Складність обчислень.
План.
1. Обчислення в кільці лишків. Алгоритм Монтгомері.
2. Обчислення з многочленами.
3. Методи множення.
4. Метод А. Карацуби.
5. Оцінка складності алгоритмів.
Ефективний шлях
багатократного приведення за модулем – використання методу Монтгомері,
запропонованого у 1985 році. Цей метод є особливо ефективном за апаратної
реалізації алгоритмів. Дуже зручно відмовитися від операцій ділення і множення
і замінити їх операціями додавання. Метод полягає в наступному. Нехай ![]() - непарне число, треба
перемножити лишки
- непарне число, треба
перемножити лишки 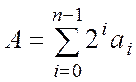 и
и ![]() . Розглянемо алгоритм:
. Розглянемо алгоритм:
R = 0;
for i = 0 until i < n do
begin
if ai = 1 then R = R + B;
if R - нечетно then R = R + N;
R = R / 2;
end
if R ³ N then R = R - N.
Сутність даного алгоритму в тому, що за рівності
A = 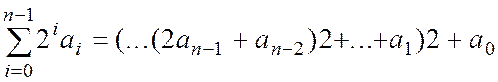
Множення числа числа В на число А зводиться до обчислення виразу
AB = ![]()
Воно
виконується за ![]() кроків, на кожному з яких виконується додавання да поточного значення
кроків, на кожному з яких виконується додавання да поточного значення ![]() значення
значення ![]() ,
, ![]() з подальшим діленням на 2. завдяки цьому діленню, отримані значення
завжди знаходяться у інтервалі
з подальшим діленням на 2. завдяки цьому діленню, отримані значення
завжди знаходяться у інтервалі ![]() . У результаті роботи даного алгоритма отримуємо число
. У результаті роботи даного алгоритма отримуємо число ![]() . Тепер для отримання числа
. Тепер для отримання числа ![]() необхідно ще раз застосувати
даний алгоритм до чисел
необхідно ще раз застосувати
даний алгоритм до чисел ![]() и
и ![]() . Оскільки число
. Оскільки число ![]() обчислюється
за допомогою зсувів і віднімань зі складністю
обчислюється
за допомогою зсувів і віднімань зі складністю ![]() двійкових операцій (його можна
обчислити зазделегідь і зберігати отримане значення), а алгоритм також
виконується за
двійкових операцій (його можна
обчислити зазделегідь і зберігати отримане значення), а алгоритм також
виконується за ![]() двійкових операцій.
двійкових операцій.
Напиклад:
Нехай А = 1´20 + 0´21 + 1´22 + 0´23 + 1´24 = 1 + 4 + 16 = 21 (10101)
В = 18
N = 41
Зрозуміло, що АВ (mod N) = 21´18 (mod 41) = 9
Обчислимо добуток цих чисел за допомогою вищенаведеного алгоритму.
1. R = 0
a0 = 1
R = R + B = 0 + 18 = 18;
R - четно;
R = R / 2 = 9.
2. a1 = 0;
R - нечетно;
R = R + N = 9 + 41 = 50;
R = R / 2 = 25;
3. a2 = 1
R = R + B = 25 + 18 = 43;
R - нечетно;
R = R + N = 43 + 41 = 84;
R = R / 2 = 42;
4. a3 = 0;
R - нечетно;
R = R + N = 1 + 41 = 42;
R = R / 2 = 21;
5. a4 = 1
R = R + B = 21 + 18 = 39;
R - нечетно;
R = R + N = 39 + 41 = 80;
R = R / 2 = 40.
Это мы получили 2-n AB(mod N)
.Теперь мы должны еще раз воспользоваться этим алгоритмом для вычисления АВ (mod N).
A’ = 22n (mod N) = 22 ´5(mod N) = 1024(mod 41) = 40 = 0´20 + 0´21 + 0´22 + 1´23 + 0´24 + 1´25
B ’= 40;
N = 41.
1. R = 0
a0 = 0
R - парне;
R = R / 2 = 0.
2. a1 = 0;
R - парне;
R = R / 2 = 0;
3. a2 = 0
R - парне;
R = R / 2 = 0;
4. a3 = 1;
R = R + B = 0 + 40 = 40;
R - парне;
R = R / 2 = 20;
5. a4 = 0;
R - парне;
R = R / 2 = 10;
6. a5 = 1;
R = R + B = 10 + 40 = 50;
R = R - N = 50 - 41 = 9.
Обернення.
Для
заданого числа ![]() ,
, ![]() , знаходимо за допомогою
розширеного алгоритма Евкліда числа
, знаходимо за допомогою
розширеного алгоритма Евкліда числа ![]() та
та ![]() , що задовільняє
рівності
, що задовільняє
рівності ![]() . Якщо
. Якщо ![]() ,
то в якості оберненого можна взяти
,
то в якості оберненого можна взяти ![]() . Таким чином, обернення
в кільці лишків можна виконати за
. Таким чином, обернення
в кільці лишків можна виконати за ![]() бітових операцій.
бітових операцій.
Ділення.
Так як 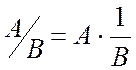 , то ділення в кільці лишків
виконується із складністю
, то ділення в кільці лишків
виконується із складністю ![]() .
.
Обчислення з многочленами. Між обчисленнями над довільним
кільцем ![]() та у кільці цілих чисел, записаних у якій-небудь системі обчислень
багато спільного. Вони виконуються за схожими формулами, а різниця полягає лише
в тому, що для чисел необхідно брати до уваги знаки переносу від молодших
розрядів до старших, у той час коли у випадку многочленів ніяких переносів при
операціях з коефіцієнтами не виникає – і початкові величини і значення лежать у
кільці
та у кільці цілих чисел, записаних у якій-небудь системі обчислень
багато спільного. Вони виконуються за схожими формулами, а різниця полягає лише
в тому, що для чисел необхідно брати до уваги знаки переносу від молодших
розрядів до старших, у той час коли у випадку многочленів ніяких переносів при
операціях з коефіцієнтами не виникає – і початкові величини і значення лежать у
кільці ![]() .
.
Складність операцій
з многочленами зазвичай оцінюють кількістю арифметичних операцій кільця ![]() , що виконуються над його
коефіцієнтами. Якщо відома складність бітової операції у полі, то можна оцінити
результуючи бітову складність операцій з многочленами. Щоб відрізняти
арифметичну складність від бітової в оцінках ми будемо використовувати символи
, що виконуються над його
коефіцієнтами. Якщо відома складність бітової операції у полі, то можна оцінити
результуючи бітову складність операцій з многочленами. Щоб відрізняти
арифметичну складність від бітової в оцінках ми будемо використовувати символи ![]() і
і ![]() .
.
Обчислення значень многочленів.
Нехай ![]() -
довільне кільце. Розглянемо добре відомий алгоритм Руфіні – Горнера для обчислення значень многочлена
-
довільне кільце. Розглянемо добре відомий алгоритм Руфіні – Горнера для обчислення значень многочлена ![]()
Над кільцем ![]() у точці
у точці ![]() .
Він базується на наступному представленні многочлена
.
Він базується на наступному представленні многочлена
![]()
і полягає у
послідовному обчисленні значень ![]() за формулами
за формулами ![]()
![]()
Останнє число ![]() і буде шуканим значенням
многочлена. Арифметична складність алгоритма, очевидно, становить
і буде шуканим значенням
многочлена. Арифметична складність алгоритма, очевидно, становить ![]() . Бітову складність у
випадку, коли у якості кільця
. Бітову складність у
випадку, коли у якості кільця ![]() розглядається кільце цілих чисел можна оцінити виразом
розглядається кільце цілих чисел можна оцінити виразом ![]() , де через
, де через ![]() позначений максимум з двох
чисел: числа двійкових знаків у записі найбільшого з коефіцієнтів і числа
позначений максимум з двох
чисел: числа двійкових знаків у записі найбільшого з коефіцієнтів і числа ![]() , а число
, а число ![]() позначає число двійкових
знаків у записі найбільшого з чисел
позначає число двійкових
знаків у записі найбільшого з чисел ![]() . Таким чином, отримуємо оцінку
. Таким чином, отримуємо оцінку ![]()
Алгоритм Руфіні
- Горнера дозволяє отримати не тілько значення ![]() . Як показує наступна
теорема, величини
. Як показує наступна
теорема, величини ![]() є коефіцієнтами многочлена, що є залишком від ділення многочлена
є коефіцієнтами многочлена, що є залишком від ділення многочлена ![]() на
на ![]() .
.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.