Використання модульної арифметики. Обчислення з многочленами. Методи множення. Складність обчислень, страница 2

Теорема. Справедлива рівність

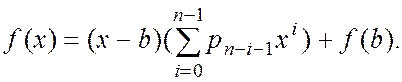
Доведення.

Маємо

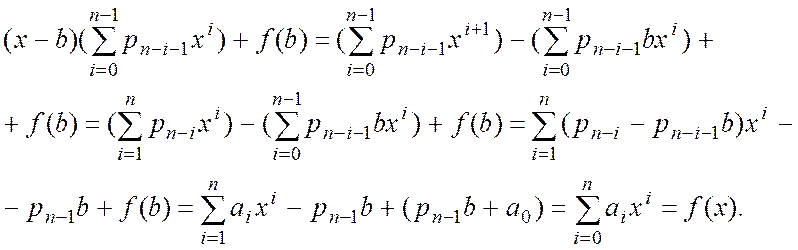
Теорема доведена.

Методи множення.

Для зручності ми будемо вважати, що оперуємо цілими числами, що виражені в двійковій системі обчислення. Ми маємо два -розрядних числа   и ,

то можна записати

де  - „найбільш значуща половина” числа, , а  - „найменш значуща”; подібним чином , .

Наприклад: Запишемо у подібній формі число

Тепер ми маємо

.

Ця формула зводить задачу множення -розрядних чисел до трьох операцій множення -розрядних чисел: . Плюс деякі прості операції зсуву і додавання. Цю формулу можна використовувати для множення з подвоєною точністю, коли результат треба отримати з четвірною  точністю. За допомогою цієї формули можна визначити деякий рекурсивной процес для множення, набагато швидший, ніж вже знайомий нам метод, коли - велике і що має час виконання  .кщо  - час, що потребує множення -розрядних чисел, то ми маємо  для деякої константи , оскільки у правій частині співвідношення треба виконати тільки три операції множення плюс деякі операції додавання і зсуву. З останнього співвідношення по індукції витікає, що ,

Якщо вибрати  достатньо великим, з тим, щоб ця нерівність виконувалась при , отримаємо

Тобто час, що витрачається на множення, можна скоротити з величини порядку  до величини порядку , і, звичайно при більшому цей алгоритм набагато швидше.

Схожий, але складніший  метод виконання множення з часом  біля  був вперше запропонований А.Карацубою.

Час виконання можна скоротити ще більше, якщо помітити, що тільки що розглянутий метод є окремим випадком (при  ) більш загального методу, який дає

 

для будь-якого фіксованого . Цей загальний метод можна отримати наступним чином. Розіб’ємо

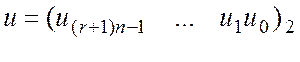    и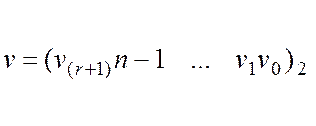     

на  часток:

            

де кожне  і кожне  є розрядними числами.

Розглянемо многочлени

,   

і припустимо

.

Так як  і , то ми маємо , і тому, якщо знати коефіцієнти  , можна легко обчислити . Задача полягає у тому, щоб знайти добрий спосіб обчислення коефіцієнтів , виконуючи лише  операцій множення -розрядних чисел плюс деякі додаткові операції, для яких час виконання пропорційний .

Цього можна досягти обчисенням .

Коефіцієнти усякого многочлена ступіня  можна записати у вигляді лінейної комбінації значень цього многочлена у  різних точок. Найбільший час, необхідний для взяття такої комбінації пропорційний  . Насправді добутки  являють собою, за сутністю, не добутки -розрядних чисел, а добутки чисел, розряд яких не перевищує  , де  - фіксована величина, що залежить від . Легко скласти програму множення для -розрядних чисел, яка потребує тільки  операцій, так як при фіксованому  два добутки -розрядних чисел на -розрядні можна отримати за  операцій. Можна показати, що для цього метода .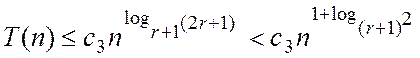

Теорема.

Для будь-якого  існує така постійна  і такий алгоритм множення, що число елементарних операцій  , що потрібне для множення двох -розрядних чисел, задовольняє оцінку .

Ця теорема ще не найкращій результат. Для практичних цілей великий недолік, що метод різко ускладнюється за  тобто . Ця теорема незадовільна і з практичної точки зору, так як у ній не повністю використовується метод многочленів, що лежить у її основі.

Перш ніж розглянути алгоритм Тоома-Кука, розберемо один приклад. На цьому прикладі нема можливості побачити фективність метода, оскільки ми маємо справу з невеликими числами. Але можна побачити деякі корисні спрощення, прийнятні і у загальному випадку.

Припустимо, що треба перемножити   та . У двійковій системі обчислення  та . Нехай . Многочлени  ,     .

Звідси знаходимо  :

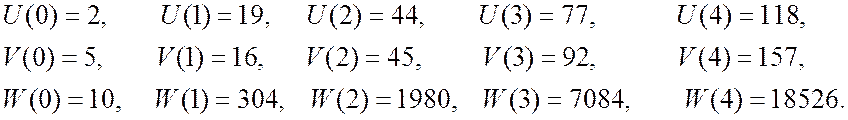(4.1)

Тепер, використовуючи п’ять останніх величин, знайдемо п’ять коефіцієнтів многочлена .

Для знаходження коефіцієнтів многочлена  при заданих значеннях  можна скористатися одним цікавим невеликим алгоритмом. Спочатку запишемо , де

 і де  невіомі, як і . Тепер

, і за індукцією знаходимо, що для всіх

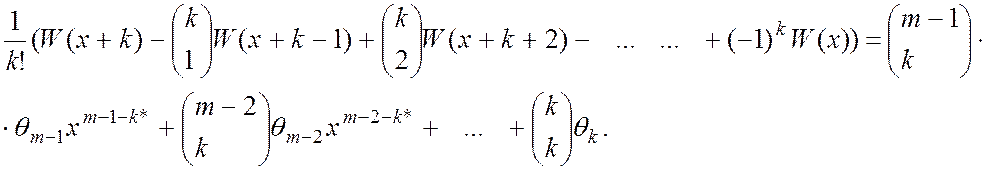
Позначаючи ліву частину выразу через 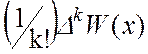 мы бачимо, що

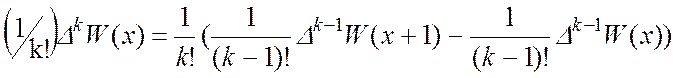
и .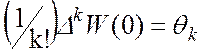

Таким чином, коефіцієнти  можна обчислити за допомогою дуже простого методу, який можна продемонструвати для многочлена , що визначений співвідношенням (4.1):

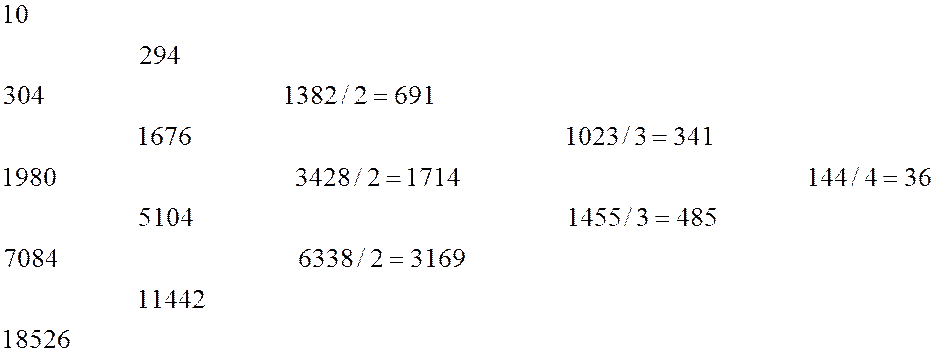
Крайня колонка складається з заданих значень ; щоб отримати -ю колонку, треба обчислити різниці між сусідніми величинами попередньої колонки і розділити їх на . Коефіцієнти  розташовані у колонках зверху; , тому ми маємо

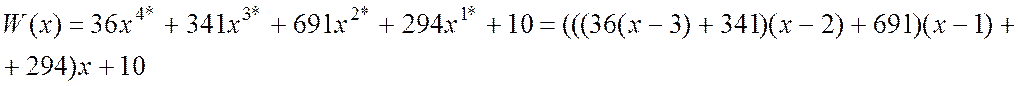В загальному вгляді можна записати

ця формула показує, яким чином з коефіцієнтів  можна отримати коефіцієнти :

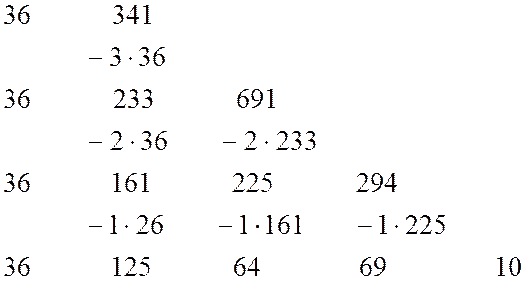
Послідовно виходять коефіцієнти многочленів  і т.і.

Згідно останньої таблиці ми маємо

Тож, відповідь  де  отримується у результаті операцій дадавання і зсуву. Крім того, якщо коефіцієнти многочлена  - невід’ємні, то такими будуть і числа , а тоді всі проміжні результати, що отримуються в процессі проведення обчислення, будуть невід’ємними.

Теорема.

Існує константа , така, що час виконання алгоритма С  менший 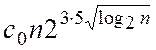  циклів.