Алгоритм Евкліда. Розширений алгоритм Евкліда. Складність алгоритмів. Складність операцій додавання і віднімання

ЛЕКЦІЯ 2

Алгоритм Евкліда. Розширений алгоритм Евкліда. Складність алгоритмів. Складність операцій додавання і віднімання.

План

1. Алгоритм Евкліда.

2. Розширений алгоритм Евкліда.

3. Оцінка складності алгоритмов.

4. Складність операцій додавання і віднімання.

5. Використання модульної арифметики.

      Нагадаємо, що два числа називають взаємнопростими, якщо вони не мають спільних дільників, крім 1. Иншими словами, якщо найбільший спільний дільник чисел  і  дорівнює 1, то то ці числа називають взаємнопростими і записують .

      Один з шляхів обчислення найбільшого спільного дільника двох чисел – використання алгоритма Евкліда. Евклід описав цей алгоритм у своїй книзі „Елементи”, датованій 300 роком до н. е. Однак алгоритм був створений не Евклідом. Історики вважають, що алгоритм на 200 років старіший. Це найдавніший нетривіальний алгоритм, що дойшов до наших днів.

      Будемо позначати найбільший спільний дільник чисел А і В через (А,В). Нагадаємо, що алгоритм Евкліда полягає у послідовному виконанні операції ділення з залишком до отримання нульового залишку. Нехай А > В > 0 . Позначимо A = r_-1 , B = r₀  і при і . Тоді  і до отримання залишка необхідно виконати  ділення.

Оцінимо число ділень, що виконується у алгоритмі Евкліда. Для цього розглянемо послідовність чисел Фібоначчі

Лема. При вірна нерівність, де .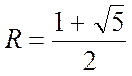

Доведення. Застосуємо індукцію за . При  тверждення є очевидним.

Далі, використовуючи припущення індукції, маємо

Так як  R є додатнім коренем рівняння

Дійсно, 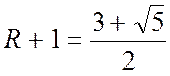 и .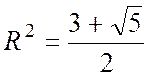

Теорема (Ламе, 1844). Для будь-якого натурального числа число ділень в алгоритмі Евкліда для знаходження найбільшого спільного дільника чисел А і В,  не перевершує  .

Доведення.

Доведемо, що при . При  вірно. Для   , пам’ятаючи про індукцію, маємо

_.

Тому, звідки виходить шукана оцінка числа ділень .

()

Безпосередньо з цієї теореми можно отримати оцінку складності алгоритму Евкліда для знаходження найбільшого спільного дільника двох n-розрядних чисел.

.

Разом з тим, цю оцінку можно уточнити, якщо звернути увагу на те, що складність операції ділення кутом числа  на число  , , насправді має вигляд . Звідси, позначаючи через  довжину запису залишку  , де  , отримаємо більш точну оцінку складності алгоритму Евкліда

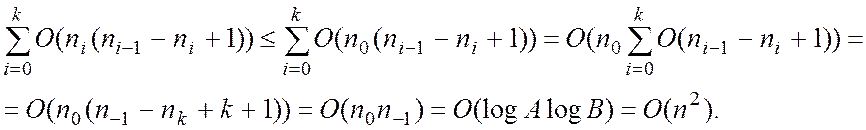
Оцінка складності алгоритму Евкліда не є оптимальною для знаходження НСД. Існує багато різних модифікацій алгоритму Евкліда. Можно, наприклад, зменшити кількість кроків алгоритму, модифікуючи алгоритм з метою зменшення абсолютних значень залишків. А саме будемо змінювати залишок остаток   на , якщо 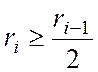. За такого виправлення виходить послідовність чисел, що задовільняє умові 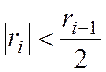. Те, що деякі з чисел будуть від’ємними не впливає на вид спільних дільників. У результаті отримуємо оцінку кількості ділень . Проте, даний підхід не покращує загальну оцінку складності модифікованого алгоритму Евкліда.

      Існують алгоритми, в яких взагалі не виконуєтьмя операція ділення. Наприклад у алгоритмі LSGCD (lift shift greatest common divisor) операція ділення з залишком замінена на лівий зсув дільника з наступним відніманням з делимого, так, що отримана послідовність на кожному кроці задовільняє умові з попереднього алгоритму.

У даному алгоритмі виконуються кроків, кожен з яких має складність , тому загальна оцінка складності маає вигляд .

      Існує алгоритм знаходження НСД з оцінкою складності , однак, його пояснення достатньо складне і тут не наводиться.

      Можно також відмітити, що алгоритм Евкліда широко використовується не тільки при визначенні спільних дільників чисел, але й поліномів. А саме, в теорії подільності його використовують при тестуванні взаємної простоти двох поліномів з коефіцієнтами, наприклад, з кінцевого поля.

Задача обчислення зворотніх значень за модулем трохи складніша. Іноді вона має розв’язок, іноді – ні. Наприклад, зворотнє значення 5 за модулем 14 дорівнює 3. З іншого боку, число 2 не має звототнього значення за модулем 14. У загальному випадку рівняння  має єдиний розв’язок, якщо  і взаємнопрості. Якщо  і не є взаємнопростими, то   не має рішень. Зворотнє значення за модулем  можно обчислити за допомогою розширеного алгоритму Евкліда.

Розглянемо цей алгоритм. Що дозволяє не тільки знаходити НСД чисел  і а ще й знаходити цілі числа  і  , що задовольняють рівності . Із звичайним алгоритмом Евкліда він різниться тим, що разом з послідовністю залишків обчислюються ще дві допоміжні послідовності  і .

Наприклад

5x +7y = НОД (5,7 )

1.  r_{- 1} = 5; r₀ = 7

x _{- 1} = 1; y _{- 1} = 0; x ₀ = 0; y ₀ = 1

d ₁ = ë r _{-  1} / r ₀  û =  ë 5 / 7 û = 0

r ₁ = r _{- 1} - d ₁ r ₀ = 5 - 0´ 7 = 5

x ₁ = x _{- 1}  - d₁ x ₀ = 1 - 0´ 0 = 1

y ₁ = y _{- 1} - d ₁  y ₀ = 0 - 0´ 1= 0

2.   d ₂ = ë r ₀  / r ₁  û =  ë 7 / 5 û = 1

r ₂ = r ₀  - d ₂  r ₁ = 7 - 1´ 5 = 2

x ₂ = x ₀   - d₂ x ₁ = 0 - 1´ 1 = - 1

y ₂ = y ₀  - d ₂  x ₁ = 1 - 1´ 0= 1

3. d ₃ = ë r  ₁ / r ₂  û =  ë 5 / 2 û = 2

r ₃ = r  ₁ - d ₃ r ₂ = 5 - 2´ 2 = 1

x ₃ = x  ₁  - d₃ x ₂ = 1 - 2´ ( - 1) = 3

y ₃ = y  ₁ - d₃  y ₂ = 0 - 2´ 1= - 2

4.  d ₄ = ë r ₂ / r ₃  û =  ë 2 / 1 û = 2

r₄ = r ₂ - d ₄ r ₃= 2 - 2´ 1 = 0

Дійсно, знайдені числа та, що задовольняють рівності

Д(5,7)