Алгоритм Евкліда. Розширений алгоритм Евкліда. Складність алгоритмів. Складність операцій додавання і віднімання, страница 2

5 ´ 3 +7´ ( - 2 ) = НОД (5,7 )

Сам алгоритм можно подати таким чином:

r_{- 1} = А; r₀ = B

x _{- 1} = 1; y _{- 1} = 0; x ₀ = 0; y ₀ = 1

for i = 1 until r _i  > 0 do

        begin

                d _i = ë r _{i - 2}  / r _{i - 1}  û ;

                r _i = r _{i - 2} - d _i  r _{i - 1} ;

                x _i = x _{i - 2}  - d _i  x  _{i - 1} ;

                y  _i = y  _{i - 2} - d  _i   y  _{i - 1} ;

                i = i + 1;

end

Значення  та ,за яких  будуть шуканими в силу наступного тверждення:

Лема.

При всіх   ,  ,виконується рівність

Застосуємо індукцію по . При  рівність очевидна.

Якщо рівності доведені для всіх значень індексів менших від, то для , користуючись індуктивним припущенням, отримуємо

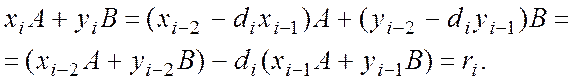
Легко побачити, що складність цього алгоритму відрізняється від складності звичайного алгоритму Евкліда не більше, ніж на константний співмножник, і складає

, где длина записи чисел и  

Використання модульної арифметики.

Модулярні обчислення нерідко використовують в криптографії, оскільки обчислення дискретних логарифмів та квадратних коренів за модулем може стати непростою задачею. До того ж, модулярну арифметику простіше реалізувати на комп’ютерах, так як вона обмежує діапазон проміжних значень результату. Для -бітових модулів довжина проміжних результатів будь-якої операції додавання, віднімання або множення не перевищує  бітів. Тому за допомогою модулярної арифметики можно, наприклад, виконати піднесення до ступіні без громіздких проміжних результатів. Обчислення ступіня деякого числа за модулем іншого числа,  являє собою просту послідовність операцій множення і ділення, однак відомі методи їх прискорення. Один з таких методів прагне мінімізувати кількість множень за модулем. Оскільки операції дистрибутивні, піднесення до ступіню виконується швідше як послідовність множень, кожного разу отримуючи лишки. Зараз ви не відчуваєте різниці, але вона стане помітною за множення 200-розрядних чисел.

      Наприклад, обчислюючи , можно не виконувати сім множень і одне величезне приведення за модулем:

.

Замість цього Виконайте три менших множення і три менших приведення за модулем:

.

Під час обчислень з цілими числами часто використовують наступне.

Якщо відомо, що початкові числа і результати обчислень обмежені деяким числом (при цьому припускають нерівності двох видів  або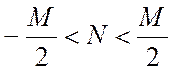), то обчислення можна проводити в кільці лишків , ототожнюючи числа з вказаних інтервалів і відповідні лишки. Щодо , то його можно вибирати різними шляхами, причому цей вибір переважно визначає складність обчислень.

Найбільш ефективним такий підхід є у випадку, коли число  може бути представлене у виді добутку невеликих взаємнопростих чисел , оскільки в даному випадку можно скористуватися ізоморфізмом кілець.

.

При цьому співвідношенні кожному числу з інтервалу  відповідає набор , де , . У даному випадку маємо на увазі найменший невід’ємний залишок від ділення числа   на число . Замість обчислень з початковими числами можно перейти до їх залишків і проводити усі обчислення в кільцях , , а потім, отримавши результат, виконати зворотній перехід і відновити шукане число за залишками.

Для виконання зворотнього переходу Застосовують китайську теорему про залишки. Більш докладно теорема про залишки розглядається у теорії чисел.

Теорема. Нехай , де    попарно взаємнопрості, і

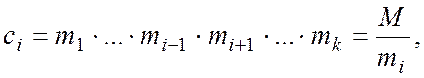
(тут і далі запис , на відміну від запису правої частини порівняння , означає найменший невід’ємний залишок від ділення числа с на число   ).

Тоді розв’язок системи порівнянь

існує однозначно за модулем М і знаходиться за формулою

.

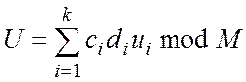Доведення легко витікає з наступних властивостей обраних чисел:

, при ,

,

Для обчислення значення u за даною формулою необхідно

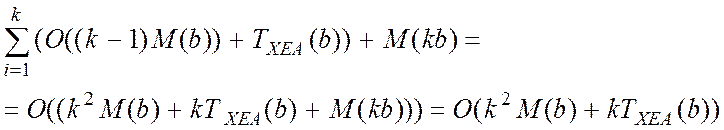
двійкових операцій, де через  позначена складність знаходження зворотнього елементу в кільці , за допомогою розширеного алгоритму Евкліда. Працемісткість можно зменшити, якщо аналогічно попередньому випадку використати техніку „розподіляй і володаруй”, застосовуючи кожного разу аналог формули за. В цьому випадку виходить оцінка  (Існує і інша формула для обчислення  u ,працемісткість така ж, але є переваги.)

      Будемо ототожнювати елементи кільця лишків  з числами з інтервалу . Нехай .

      Додавання, віднімання.

Під час складення чисел в інтервалі . Сума  може вийти за межі інтервалу, тому може знадобитися ще одне віднімання . ( 13 (mod 17) + 8 (mod 17) = 13 + 8 -17 = 4 (mod 17 ))Аналогічно, під час віднімання може знадобитися ще одне додавання . (7 (mod 13) - 12 (mod 13) = 7 - 12 + 13 = 8 (mod 13 )). Тому, складність цих операцій дорівнює .

      Множення.

      Для знаходження лишку, що відповідає добутку двох лишків, треба виконати одне множення -розрядних чисел і одне ділення -розрядного числа на -розрядне. Тому, складність даної операції дорівнює .

Вадою модулярного представлення є те, що порівняно складно перевірити, чи є число додатнім або від’ємним. Важко також перевіряти, у результаті якої дії відбувається переповнення – додавання, віднімання або множення, і доволі складно ділити. Використання модулярної арифметики вигідне тільки якщо у розпорядженні є засоби швидкого переходу до модулярного стану та навпаки.