Системы дифференциальных уравнений. Системы линейных дифференциальных уравнений. Метод Коши, страница 3

Так как функции  - решение однородной системы ДУ (1).

 Умножим (6) скалярно на : , ,

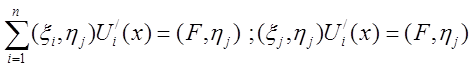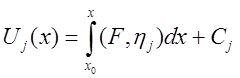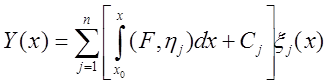 .                                                                         (7)

Метод Коши применяется, когда мы можем построить две взаимно ортогональных системы нормальных фундаментальных решений.

       Системы линейных дифференциальных уравнений с  

                       постоянными коэффициентами

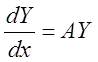,                                                                                                            (1)

где - матрица с постоянными коэффициентами.                                                                                                                       

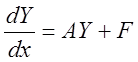                                                                                                                                                                                        (2)

неоднородная система ДУ.

Решение (1) будем искать в виде ,                                                                                                                                      (3)

где  - вектор, .

Подставив решение в (1), получим:   - -собственные значения, - собственные векторы.

1. Все корни характеристического уравнения действительны и различны. Это значит,  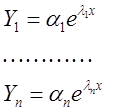- - частные решения однородной системы.

следовательно, общее решение однородной системы имеет следующий вид:                                                                                                                            (4)

Воспользуемся основной теоремой алгебрыо представлении вещественной матрицы:

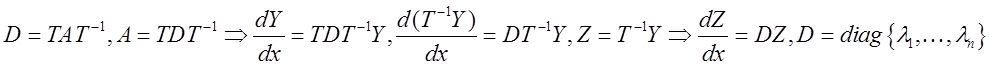
Проинтегрировав систему 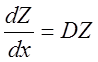 покомпонентно, получаем: . Тогда общее решение однородной системы ДУ  , где матрица  состоит из собственных векторов матрицы  А.

2. Характеристическое уравнение имеет комплексный корень .

Если матрица  вещественная, то будет существовать комплексно сопряженный корень характеристического уравнения. Общее решение (1) может быть представлено в виде (4).

Согласно следующей теореме:

 Теорема. Если оператор 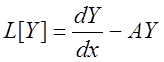- вещественный, а -функции принимающие действительные значения, а  -решение однородного уравнения , тогда  будут тоже действительными решениями .

То есть, если  вещественная матрица, то паре комплексно сопряженных корней характеристического уравнения будет соответствовать пара действительных решений, а именно: .

3. Корень характеристического уравнения   имеет кратность .

В этом случае  для  матрицы  строится  Жорданова Нормальная Форма и общее решение СЛДУ имеет вид: , постоянные векторы. Максимальная степень полинома соответствует максимальной степени элементарного делителя для характеристического числа .

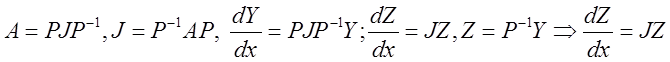, -соответствующая Жорданова Нормальная Форма. Допустим, что у нас есть одна клетка Жордана размерности , соответствующая собственному числу :

   .

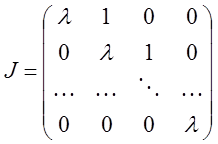   Тогда покомпонентно система 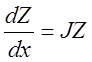   будет иметь вид:

   

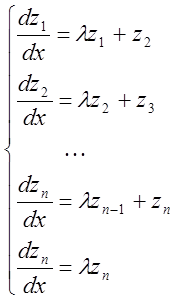
Начнем интегрировать эту систему с -го уравнения:

.

Затем решим -ое уравнение методом вариации постоянных, используя уже известное решение .

.

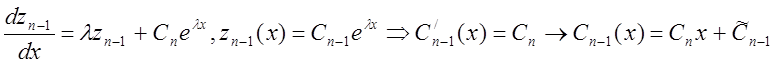Продолжая процесс интегрирования получим все компоненты вектора .

Общее решение однородной системы ДУ имеет вид: , где матрица Р состоит из собственных и присоединенных векторов матрицы А, соответствующих собственному числу .

Матричные дифференциальные уравнения.

Пусть дано матричное дифференциальное уравнение: 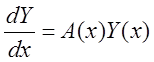,         (1)