Системы дифференциальных уравнений. Системы линейных дифференциальных уравнений. Метод Коши, страница 2

Теорема 3. Если это решение системы (8), а решение системы (9), тогда + будет тоже решение (8).

Доказательство: По свойствам линейного оператора: g

Теорема 4. Общее решение (8) на отрезке  с непрерывными на этом отрезке коэффициентами  и правыми частями  равно сумме общего решения соответствующей однородной  системы (9)  и частного решения неоднородной системы (8).

Доказательство: Так как условия теоремы о существовании и единственности выполнены, следовательно, остается доказать, что 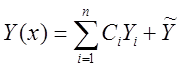  будет удовлетворять произвольно заданным начальным значением (7), то есть 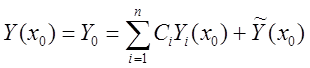.                                                                                                                              (11)

 Для системы (11) всегда можно  определить значения . Это можно сделать так как  - фундаментальная система решений.g

Теорема 5(принцип суперпозиции). Решение системы Дифференциальных Уравнений вида 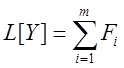 может быть представлено в виде 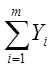, каждое из которых удовлетворяет уравнению ,тогда .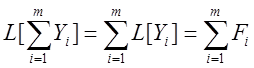

Замечание. Принцип суперпозиций можно распространить на случай  при условии, что ряд составленный из , сходится и допускает почленное дифференцирование.

Метод вариациипостоянной

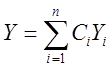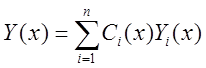Пусть  - общее решение однородной системы (9). Будем искать решение (8) в следующем виде: , где  - неизвестные функции. Подставим решение  в (8): 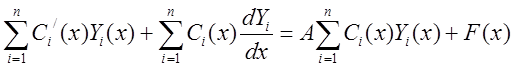, при этом учтем, что  - решения (9), то есть 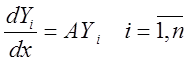.  Получаем, 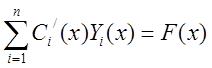- векторное уравнение. Последнее соотношение можно записать в виде n-уравнений с n- неизвестными  . При этом  на , так как  - фундаментальная система решений (9) и, следовательно, мы можем однозначно определить неизвестные функции:

.                                                                                                 (12)

.                                                                                                   (13)

И тогда общее решение (8) будет иметь вид:  .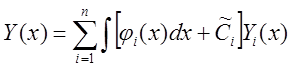

Метод Коши

Пусть дана неоднородная система  ЛДУ: 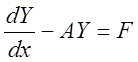                                    (1)

Нормальная фундаментальная система решений, соответствующая системе (1) известна:

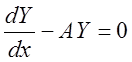                                                                                                                                                                                             (2)

И известна нормальная фундаментальная система решений системы 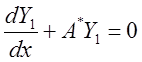(3):

                                                                                                                                                                                               (3)

 Система (3) называется сопряженной к системе (2).

Пусть  -  нормальная фундаментальная система решений (2);  - нормальная фундаментальная  система решений (3).

Начальные условия - . Скалярное произведение . Покажем, что во всех точках отрезка , скалярное произведение равно , то есть

                                                                                         (4)

 Покажем, что , .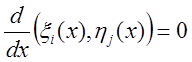

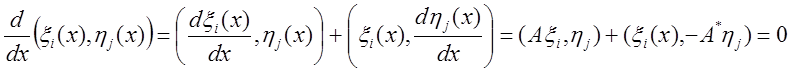Построим решение нашего Дифференциального Уравнения методом Коши. Будем его искать в виде: 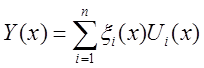,                                                                                                                                                                                                                (5)

 где - неизвестные скалярные функции. Подставим (5) в (1):

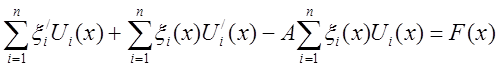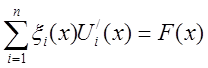, .                                                                                                        (6)