Математика \ Специальные главы математики

Решение 15 заданий с множествами и подмножествами (Вариант 17)

Страницы работы

6 страниц (Word-файл)

Скачать файл

Содержание работы

Вариант 17

Задание №1

Доказать, что:

a) AÈBC AÍC и BC

Доказательство:

Пусть AÈB Í C, тогда по определению AÍC и BÍC

Пусть xÎA, yÎB, Þ xÎC и yÎC, Þ xÎAÈB, yÎAÈB Þ AÈBÍC

b) AÍBÇC AÍB и AÍC

Þ Пусть xÎA Þ xÎBÇC Þ xÎB, xÎC Þ AÍB, AÍC

Ü Пусть xÎA Þ xÎB, xÎC Þ xÎBÇC Þ AÍBÇC

c) AÇB Í C AÍ(-B)ÈC

Þ Пусть xÎAÇB Þ xÎA, xÎB, xÎC, т.к. AÇBÍC Þ xÎ(-B)ÈC Þ AÍ(-B)ÈC

Ü Пусть xÎA, xÎ(-B)ÈC Þ

1◦ xÎ(-B), xÏC, xÏB Þ AÇB = Æ, AÇBÍC

2◦ xÎC, xÏ(-B), xÎA Þ xÎB, xÎAÇB, xÎC Þ AÇBÍC

d) AÍBÈC AÇ(-B) Í C

Þ Пусть xÎA Þ xÎBÈC

1◦ xÎB, xÏC Þ xÏ(-B) Þ AÇ(-B) = Æ Þ AÇ(-B) Í C

2◦ xÏB, xÎC, xÎA Þ xÏ(-B), xÎAÇ(-B). т.к. xÎAÇ(-B) Þ AÇ(-B) Í C

Ü Пусть xÎAÇ(-B)

xÎA, xÎ(-B), xÎC (т.к. AÇ(-B) Í C) Þ xÏB

xÎA, xÎC, xÏB Þ xÎBÈC Þ AÍBÈC

Задание №2

Какие из утверждений верны для всех A,B и C?

a) Если AÎB и BÎC, то AÎC

Если AÎB, то B = {A}

Если BÎC, то C = {B} = {{A}}, то AÏC

Ответ: неверно

b) Если AÍB и BÎC, то AÎC

A,B – множества

C = {B} AÏC

Ответ: неверно

c) Если AÇB Í -C и AÈC Í B, то AÇC = Æ

Пусть xÎAÇB Þ xÎA, xÎB и т.к. AÇBÍ-C, то xÎ-C Þ xÏC

xÎA, xÏC Þ AÇC = Æ

Ответ: верно

d) Если A≠B и B≠Сб то A≠C

К примеру, возьмем A=C. A≠B, C≠B Þ неверно

Ответ: неверно

e) Если AÍ-(BÈC) и BÍ-(AÈC), то B=Æ

Пусть xÎA Þ xÎ-(BÈC) Þ xÏB, xÏC

Значит из первого выражения следует, что то, что принадлежит A не принадлежит B

Пусть yÎB Þ yÎ-(AÈC) Þ yÏA, yÏC

Вывод: можно найти такой y, который будет принадлежать B

Ответ: неверно

Задание №3

Решить систему уравнений:

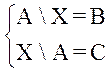
A, B, C – множества, BÍA и AÇC = Æ

X \ A = C Þ A = CÈAÇX (очевидно, если изобразить графически)

AÇX = A \ (A \ X), т.к. A \ X = B, то AÇX = A \ B. Значит, X=CÈA\B

Ответ: X = CÈA\B

Задание №4

Доказать, что:

(AÇB) ´ (CÇD) = (A´C) Ç (B´D)

Þ Пусть xÎ(AÇB) ´ (CÇD)

т.к. x = <y,z>, то yÎAÇB, zÎCÇD Þ yÎA, yÎB, zÎC, zÎD Þ x=<y,z> Î A´C, xÎB´D Þ

xÎ(A´C) Ç (B´D)

Ü Пусть xÎ(A´C)Ç(B´D)

xÎA´C, xÎB´D

yÎA, zÎC, yÎB, zÎD

yÎ(AÇB), zÎ(CÇD) Þ x=<y,z>Î(AÇB)´(CÇD) Þ xÎ(AÇB)´(CÇD)

Задание №5

Доказать, что:

a) (A\B) ´ C = (A´C) \ (B´C)

Þ Пусть x=<y,z> Î (A\B)´C Þ yÎA\B, zÎC Þ yÎA, yÏB, zÎC Þ x=<y,z>ÎA´C, x=<y,z>ÏB´C Þ xÎ(A´C) \ (B´C)

Ü Пусть xÎ(A´C) \ (B´C) Þ xÎA´C, xÏB´C Þ yÎA, zÎC, xÏB´C Þ yÎA, zÎC, yÏB Þ yÎ(A\B), zÎC Þ x=<y,z>Î(A\B) ´ C

b) A´(B\C) = (A´B) \ (A´C)

Þ Пусть xÎA´(B\C)

yÎA, zÎB\C Þ yÎA, zÎB, zÏC

x=<y,z> Î A´B, xÏA´C Þ xÎ(A´B) \ (A´C)

Ü Пусть xÎ(A´B) \ (A´C)

xÎA´B, xÏA\C

yÎA, zÎB, xÏA\C Þ yÎA, zÏС Þ zÎ(B\C) Þ x=<y,z>ÎA´(B\C)

c) A´B = (A´D)Ç(C´B), где AÍC и BÍD

Þ Пусть xÎA´B Þ yÎA, zÎB

т.к. AÍC, то yÎC

т.к. BÍD, то zÎD

yÎA zÎB

yÎC zÎD

x=<y,z>ÎA´D, x=<y,z>ÎC´B Þ xÎ(A´D)Ç(C´B)

Ü Пусть xÎ(A´D)Ç(C´B) Þ xÎ(A´D), xÎ(C´B) Þ yÎA, zÎD, yÎC, zÎB Þ xÎA´B

d) U²\(A´B) = [(U\A) ´ U] È [U ´ (U\B)]

Þ Пусть xÎU²\(A´B) Þ xÎU², x≠A´B Þ xÎU´U, xÏA´B Þ yÎU, zÎU

xÏA´B:

1◦ yÏA, zÎB Þ т.к. yÎU, yÏA Þ yÎB

yÎU, zÎU, yÏA Þ yÎ(U\A)

x=<y,z>Î[(U\A)´U] Þ xÎ[(U\A)´U]È[U´(U\B)]

2◦ yÎA, zÏB Þ т.к. zÎU, zÏB Þ zÎA

yÎU, zÎU, zÏB Þ zÎU\B Þ xÎU´(U\B) Þ xÎ[(U\A)´U]È[U´(U\B)]

Ü Пусть xÎ[(U\A)´U]È[U´(U\B)]

1◦ xÎ[(U\A)´U]

yÎU\A Þ yÎU, yÏA, zÎU. т.к. yÎU, zÎU Þ xÎU², yÏA Þ xÏA´B Þ xÎU²\(A´B)

2◦ xÎ[U´(U\B)]

yÎU, zÎU, zÏB Þ x=<y,z>ÎU², xÏA´BÞxÎU²\(A´B)

Задание №6

Пусть A и B – конечные множества, состоящие из m и n элементов соответственно:

a) Сколько существует бинарных отношений между элементами A и B?

Решение:

Мощность множества A´B = m*n, т.к. каждому элементу из A можно поставить в соответствие n элементов из множества B. А всего бинарных отношений будет столько же, сколько подмножеств в множестве пар A´B. Это число равно 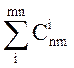2^mn

= 2^mn

Ответ: 2^mn

b) Сколько имеется функций из A в B?

По определению функции – одному аргументу соответствует только одно значение функции, а значению функции может соответствовать несколько аргументов, то искомым количеством будет число размещений элементов из B в по элементам из A с повторениями, т.е. = n^m