



Определение. Пусть ![]() - это (бес-) конечный промежуток
вещественной оси
- это (бес-) конечный промежуток
вещественной оси ![]() . Функция
. Функция ![]() называется первообразной
для функции
называется первообразной
для функции ![]() на
множестве
на
множестве ![]() , если
справедливо соотношение
, если
справедливо соотношение ![]() .
.
1) Если
функция ![]() является
первообразной для функции
является
первообразной для функции ![]() ,
то функция
,
то функция ![]() непрерывна на
промежутке
непрерывна на
промежутке ![]() .
.
2) Пусть
функция ![]() является
первообразной для функции
является
первообразной для функции ![]() .
Для того, что функция
.
Для того, что функция ![]() тоже была первообразной для функции
тоже была первообразной для функции ![]() (
(![]() ) необходимо и достаточно, чтобы
) необходимо и достаточно, чтобы ![]() .
.
3) Если
функция ![]() является
первообразной для
является
первообразной для ![]() , то любая функция
вида
, то любая функция
вида ![]() тоже является
первообразной для
тоже является
первообразной для ![]() .
.
Определение. Вся совокупность первообразных функции ![]() называется ее неопределенным
интегралом:
называется ее неопределенным
интегралом: ![]() .
.
Свойства неопределенного интеграла:
1) Операция
дифференцирования и операция нахождения неопределенного интеграла являются
взаимообратными: ![]() .
.
2) Производная
неопределенного интеграла равна подинтегральной функции: 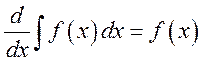 .
.
3) Если ![]() и
и ![]() интегрируема, то
интегрируема, то ![]() .
.
4) ![]() , если существуют оба интеграла
правой части.
, если существуют оба интеграла
правой части.
5) Если
функция ![]() является
интегрируемой и имеет первообразную
является
интегрируемой и имеет первообразную ![]() ,
то
,
то 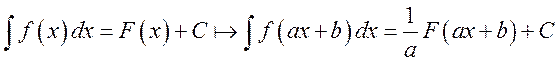 .
.
Теорема. Пусть функция ![]() определена на промежутке
определена на промежутке ![]() , а функция
, а функция ![]() - на
- на ![]() . Пусть эти функции таковы, что
образ промежутка
. Пусть эти функции таковы, что
образ промежутка ![]() является
подмножеством промежутка
является
подмножеством промежутка ![]() .
И пусть функция
.
И пусть функция ![]() дифференцируема
на промежутке
дифференцируема
на промежутке ![]() , а функция
, а функция ![]() интегрируема
на
интегрируема
на ![]() . Тогда справедливо:
. Тогда справедливо: ![]() .
.
Доказательство. Т.к. имеет место, ![]() и
и ![]() , то
, то ![]() определена всюду на
определена всюду на ![]() . Т.к.
. Т.к. ![]() является первообразной для
является первообразной для ![]() , то по определению получаем, что
она определена на
, то по определению получаем, что
она определена на ![]() , а также дифференцируема
на нем. Тогда сложная функция
, а также дифференцируема
на нем. Тогда сложная функция ![]() определена
всюду на
определена
всюду на ![]() и является
дифференцируемой на этом промежутке, как суперпозиция двух дифференцируемых
функций. Найдем производную
и является
дифференцируемой на этом промежутке, как суперпозиция двух дифференцируемых
функций. Найдем производную 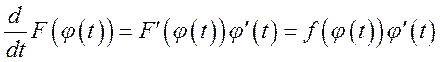 .
.
Теорема. Пусть функции ![]() определены и дифференцируемы на
промежутке
определены и дифференцируемы на
промежутке ![]() и пусть
существует
и пусть
существует ![]() , тогда
существует
, тогда
существует ![]() .
.
Доказательство. Т.к. ![]() определены
и дифференцируемы на
определены
и дифференцируемы на ![]() по
определению, то их произведение
по
определению, то их произведение ![]() также
определено и дифференцируемо на
также
определено и дифференцируемо на ![]() .
Получаем, что
.
Получаем, что ![]() . Интегрируя это
соотношение, получаем, что
. Интегрируя это
соотношение, получаем, что ![]() .
Т.к. по свойству
.
Т.к. по свойству ![]() , получаем
, получаем ![]() . Оба слагаемых в правой части
существуют, следовательно, существует и соотношение из левой части.
. Оба слагаемых в правой части
существуют, следовательно, существует и соотношение из левой части.
Определение. Дробно-рациональной функцией называется функция, являющаяся отношением двух полиномов.

![]() - вещественные
корни;
- вещественные
корни; ![]() - несуществующие
вещественные корни.
- несуществующие
вещественные корни.
Основная теорема алгебры. Любой полином ![]() -ой степени имеет ровно
-ой степени имеет ровно ![]() корней (возможно комплексных) с
учетом кратности. При этом, если все коэффициенты полинома вещественны, то его
комплексные корни будут образовывать сопряженные пары.
корней (возможно комплексных) с
учетом кратности. При этом, если все коэффициенты полинома вещественны, то его
комплексные корни будут образовывать сопряженные пары.
Определение. Величины ![]() называются кратностями корней
полинома.
называются кратностями корней
полинома.
Теорема. Если знаменатель функции ![]() представляется в виде
представляется в виде ![]() , то функция может быть представлена
в виде
, то функция может быть представлена
в виде 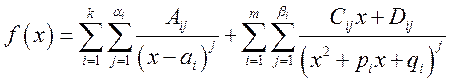 .
.
Следствие. В силу линейности интеграла имеет место
формула 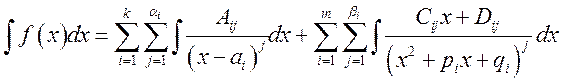
1)
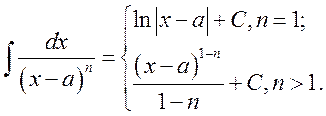
2) 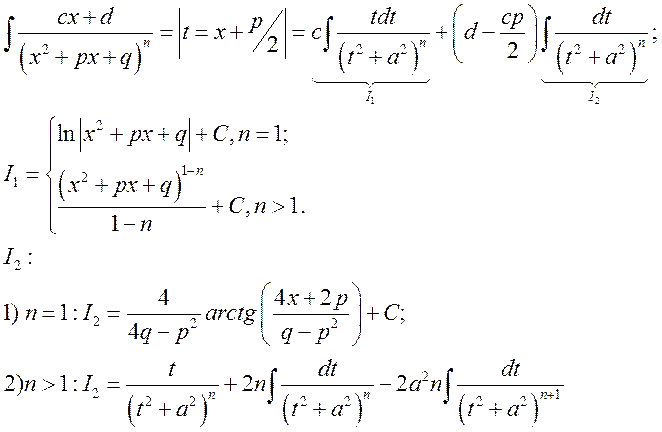
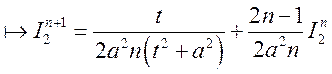 - формула понижения степени.
- формула понижения степени.
Замечание. В результате интегрирования любой
дробно-рациональной функции получается выражение, в которое входи три типа
функций: дробно-рациональные, логарифмы, арктангенсы. Причем за присутствие в
результате интегрирования в конечном выражении логарифмов и арктангенсов
отвечают дроби вида: 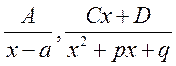 .
.
Определение. Говорят, что логарифмы и арктангенсы, образованные в результате интегрирования дробно-рациональной функции, вместе взятые, образуют трансцендентную часть, а все прочие функции – рациональную.
Форму, лежащая в основе метода Остроградского, имеет
следующий вид 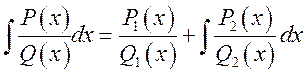 , где
, где ![]() - рациональная часть интеграла,
- рациональная часть интеграла, ![]() - трансцендентная.
- трансцендентная.
Краткий алгоритм метода:
1)
найти ![]() ;
;
2)
с помощью алгоритма Евклида: ![]() ;
;
3)
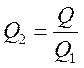 ;
;
4)
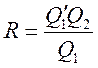 ;
;
5)
![]() ;
;
6)
Записать ![]() с
неопределенными коэффициентами.
с
неопределенными коэффициентами.
7) Найти все
неопределенные коэффициенты из ![]() .
.
1)
![]()
·
![]() ;
;
·
![]() ;
;
·
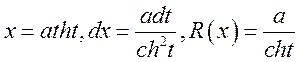 .
.
2)
![]()
·
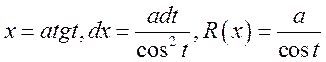 ;
;
·
![]() .
.
3)
![]()
·
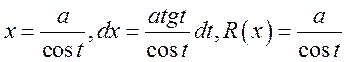 ;
;
·
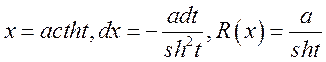 ;
;
·
![]() .
.
Замечание. Если радикал ![]() присутствует
в числителе дроби, то обычно пользуются тригонометрическими подстановками, если
в знаменателе – гиперболическими.
присутствует
в числителе дроби, то обычно пользуются тригонометрическими подстановками, если
в знаменателе – гиперболическими.
Любой интеграл от рационально-тригонометрической и рационально-гиперболической функции может быть сведен к интегралу дробно-рациональной функции с помощью двух следующих универсальных подстановок:
1)
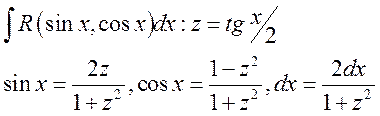 ;
;
2)
 .
.
Если же:
1)
![]() ;
;
2)
![]() ;
;
3)
![]() .
.
Подстановки Эйлера
Пусть ![]() -
дробно-рациональная функция. Пусть коэффициенты
-
дробно-рациональная функция. Пусть коэффициенты ![]() - не полный квадрат:
- не полный квадрат: 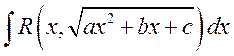 . Если
. Если ![]() , то воспользуемся заменой
, то воспользуемся заменой ![]() .
.
1ая подстановка. ![]()
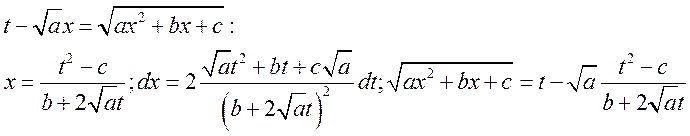
2ая подстановка. ![]()
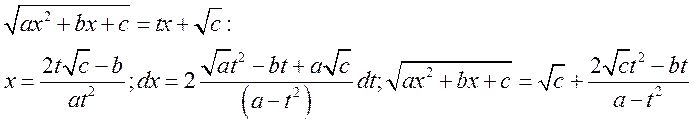
3я подстановка. Если ![]() имеет два
вещественных корня.
имеет два
вещественных корня.
![]()

Выражение под радикалом должно быть больше нуля.
Интеграл от дифференциального бинома (биноминального дифференциала)
Определение. Дифференциальный бином – это
бином вида ![]() , причем из них
хотя бы один не целый.
, причем из них
хотя бы один не целый.
Теорема Эйлера-Чебышева. Интеграл от дифференциального бинома может быть сведен к интегралу от дробно-рациональной функции в трех и только трех случаях:
1)
![]() ;
;
2)
 ;
;
3)
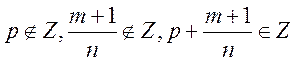 .
.
Замечание. Во всех случаях, когда ![]() , знак «-» будем считать отнесенным
к числителю.
, знак «-» будем считать отнесенным
к числителю.
Доказательство.
1)
![]()
·
![]() - бином
Ньютона.
- бином
Ньютона. 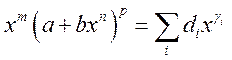 ;
;
·
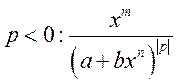 . Если
. Если ![]() , то выражение сводится к
дробно-рациональному. Если
, то выражение сводится к
дробно-рациональному. Если ![]() ,
то интеграл сводится к дробно-рациональному заменой:
,
то интеграл сводится к дробно-рациональному заменой: ![]() .
.
2)
 :
: 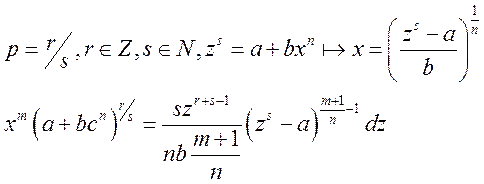
3)
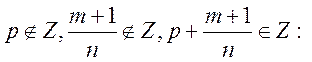
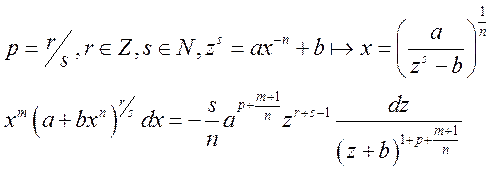
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.