Процедура определения места повреждения на языке программирования Matlab

5. ПРОЦЕДУРА ОПРЕДЕЛОЕНИЯ МЕСТА ПОВРЕЖДЕНИЯ

5.1. Целевая функция

          На языке программирования Matlab была написана процедура определения места повреждения (ОМП). Она оформлена в виде скрипта и размещена в отдельном файле. Пользователь вызывает скрипт командой.В  В её основе процедуры ОМП лежит принцип минимизации целевой функции (ЦФ), значения которой зависят о расстояния до точки КЗ и проводимости закоротки. Целевая функция сформируетсяована как норма разности 6-мерных векторов токов по концам линии: один вектор содержит токи, сгенерированные моделью, а другой – рассчитанные из уравнения установившегося режима в для конкретных значения расстоянияй до местакак зависимость от расстояния до точки поврежденияя и переходных проводимостяхей.

          Целевая функция costF находится в процедуре с названием CelFun, которая вызывается изв процедурые минимизации.

costF=norm(Iras(1:6)-I)

norm – норма;

Iras – расчётные значения токов;

I – токи, сгенерированные моделью.

5.2. Расчёт погонных параметров линии, представленной П-образной схемой замещения

5.2.1 Математическая модель линии

При разработке и программной реализации алгоритма ОМП приняты следующие допущения:

1.  Линия описывается не обобщёнными электрическими, а конструктивными параметрами.

2.  Известны все или некоторые параметры аварийного режима по обоим концам линии.

3.  Линия однородна вдоль длины.

4.  Она не имеет электромагнитных связей с другими ВЛ.

5.  На ВЛ отсутствуют грозозащитные тросы.

6.  Фазные провода расположены параллельно поверхности земли, не расщеплены, имеют круглое сечение, которое мало по сравнению с междуфазными расстояниями и расстоянием до земли.

7.  Линия настолько коротка, что её обобщённые параметры можно получить, умножив погонные параметры на длину.

          При использовании метода схем замещения реальные элементы сети представляются в виде двухполюсников для прямой, обратной и нулевой последовательностей. На такое представление ориентированы современные программы расчета установившихся режимов. В них неявно предполагается циклическая симметрия матриц проводимостей всех элементов и, конечно, их свойство быть 3-фазными. В то же время фазы реальных линий находятся не в одинаковых условиях. При расчёте несимметричных режимов большие возможности предоставляет концепция фазных координат. Параметры элементов сети в фазных координатах естественным образом формируются по конструктивным данным.

          В конечном итоге,  однородная ВЛ, на которой произошло КЗ, представляется двумя однородными участками с неоднородностью в месте повреждения. Каждый из участков представляется матрицей узловых проводимостей в фазных координатах. Исходными данными для формирования этой матрицы служат конструктивные параметры ЛЭП.

          Если принять оговорённые выше допущения, то однородный участок описывается телеграфными уравнениями, решение которых имеет вид:

где:   –- комплексы напряженийе и токов в начале линии,  –- комплексы напряженийе и токов в конце линии,  - матрицы погонных параметров.

          Квадратные матрицы коэффициентов распространения и волновых сопротивлений вычисляются по формулам:

,

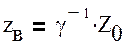
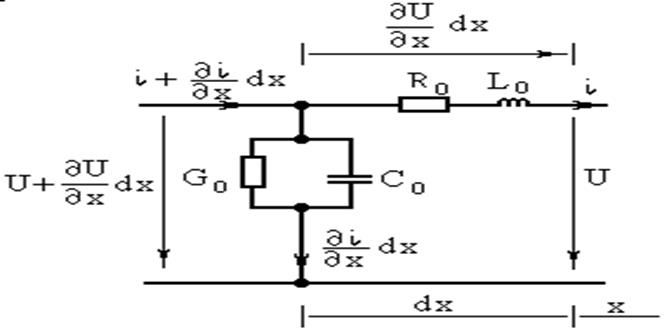Рис.5.2.1. Схема замещения однородного участка линии

Участок линии при этом рассматривается как цепочка бесконечно большого числа элементарных участков длинной dx, которые характеризуются квадратными матрицами погонных активных сопротивлений R0, индуктивностей L0, активных проводимостей G0 и емкостей С0, порядок которых равен числу фаз линии [].

Короткую линию можно представить П-образной схемой замещения, продольные сопротивления  которой можно определить, умножив на длину ее продольные погонные сопротивления. Поперечные проводимости определим, умножив погонные поперечные проводимости на половину длины участка ВЛ.

Итак, поврежденную линию будем описывать уравнением:Y_yy∙U_y=I^y, где Y_yy – матрица узловых проводимостей цепочки из двух участков повреждённой линии и включенного между ними однополюсника, моделирующего КЗ, I^y – вектор узловых токов, U^y – вектор узловых напряжений.

5.2.2 Конструктивные параметры линии

Введём обозначения и поясним смысл конструктивных параметров линии, используемых при построении математической модели. В соответствии с заданием, предметом анализа является 1-цепная 3-фазная ЛЭП без грозозащитных тросов, представленная на рис.5.2.2.

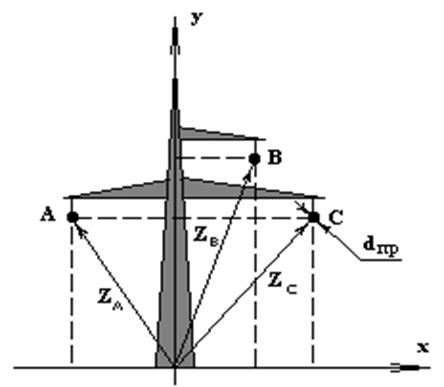          Для хранения информации о координатах проводов воспользуемся векторами координат Х и Y, число элементов которых соответствует количеству фаз исследуемой линии, т.е. трем. Каждый элемент вектора представляет собой значение проекции вектора Z, соединяющего начало координат (точка установки опоры на поверхности земли) и ось провода. Также используются некоторые справочные данные о характеристиках самого провода, такие как: проводимость алюминия, магнитная проницаемость проводов, погонные потери мощности на корону.