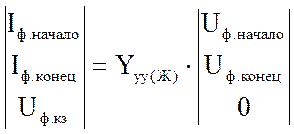Другие предметы \ Автоматизация проектирования и управления электроснабжения электрических сетей

Процедура определения места повреждения на языке программирования Matlab, страница 3


  Нам известны напряжения по обоим концам ЛЭП, а также известно, что узловой ток в месте короткого замыкания равен нулю. Для расчета токов по обоим концам поврежденной ВЛ выполним следующие действия: Выполним шаг исключения Жордана, выбрав в качестве опорного элемент матрицы Yyy, соответствующий узлу КЗ (исключаем неизвестное напряжение в точке КЗ). Получим:

Yyy(Ж) - матрица Yyy после преобразования Жордана

          Расчётные значения токов определяются с помощью функции, зависящей от расстояния до точки КЗ, проводимости закоротки и номера топологического вектора, характеризующего тип КЗ.

Iras=Rasch_znach(lYkz(1),lYkz(2),num)

          где lYkz – вектор, состоящий из двух элементов: расстояния до места повреждения и проводимости закоротки. num – номер топологического вектора, характеризующего тип КЗ.

Текст процедуры расчёта токов:

function I=Rasch_znach(l,Ykz,num)

          global f_nom

global Fsp

          global Fps             гобальныеглобальные переменные

          global U

globalL

load('ReU1');load('ImU1');       чтение из файлов сгенерированных напряжений load('ReU2'); load('ImU2');          начала и конца линии.

j=size(ReU1,2)-5;  вычисляем размерность матрицы действительных значений напряжений, записанной в файл ReU1.

U12=[complex(ReU1(2:4,j),ImU1(2:4,j)); complex(ReU2(2:4,j),ImU2(2:4,j))]; из сгенерированных файлов осциллограмм берём столбец напряжений фаз.

Задаём конструктивные параметры линии:

X1=[-2 3.3 2]; Y1=[13;13;17];  координаты подвески проводов, (м)

F=95;  сечение провода, (мм2)

Pk=5;  потери мощности на корону, (кВт/км)

L=20;  длина линии, (км)

U=abs(U12(1:1));  номинальное напряжение линии, (кВ)

r=sqrt(F/pi);  сечение провода, (м)

[Z0 Y0]=Pogon_Par(X1, Y1, F, Pk, U, f_nom, r); рассчитываем погонные параметры линии.

Yyy=SintezY(l,Z0,Y0,L,Ykz,num);  формируем матрицу узловых проводимостей

Uf1=U12(1:3); фазные напряжения в начале линии.

Uf2=U12(4:6);  фазные напряжения в конце линии.

y=Jord(Yyy);  исключаем узел на стыке между начальным и конечным участками, выполнив шаг жордановых исключенийосуществление шага Жордана.

Uy={Uf1;Uf2;[0;0;0]};   матрица напряжений в фазных координатах по концам линии

Uyy=CellArrayToVector(Uy); преобразование блочного вектора в обычный

Yy=CellArrayToMatrix(y); преобразование блочной матрицы в обычную

I = Yy*Uyy;  определяем токи в фазных координатах по концам линии

          Процедуры расчета погонных параметров, формирования матрицы узловых проводимостей, осуществления шага Жордана и процедуры преобразования блочных векторов и матриц (под блочной матрицей в данном случае понимается квадратная матрица, каждый элемент которой представляет собой так же квадратную матрицу) были взяты в виде процедур, написанных в MathCad-документе выпускником 2003 года Константином Перемибедой. Все эти процедуры были переложены на язык программирования Matlab. Тексты данных программ приведены в приложении. Процедуры преобразования блочных векторов и матриц в обычные необходимы, так как в Matlab не предусмотрены арифметические операции над блочными массивами.

5.5. Минимизация целевой функции

          В качестве метода минимизации используется процедура локальная минимизация, имеющаяся в библиотеки Matlab. Данная процедура ищет минимум функции n переменных с ограничениями. Процедура минимизации имеет следующий синтаксис:

x = fmincon(fun, x0, A, b, Aeq, beq, lb, ub)

          где fun – имя целевой функции; х0 – вектор стартовых значений (в качестве стартового значения расстояния до места повреждения целесообразно указать середину линии); lb и ub – нижняя и верхняя граница изменения х (lb ≤ x ≤ ub). Расстояние до места повреждения не может быть меньше нуля и больше длины линии, а значение переходной проводимости лежит в пределах от 0 до 2. А, Aeq – матрицы коэффициентов, b, beq – вектора свободных членов в неравенствах и уравнениях ограничения (A∙x ≤ b, Aeq∙x = beq). При отсутствии данных ограничений на их месте ставятся следующие значения: A=[], Aeq=[], b=[], beq=[] (на Matlab′е это означает пустую матрицу, т.е. матрицу с нулевым число элементов).

Текст процедуры ОМП:

function x=Procedura_FPF() название процедуры

global I

global U

global Fsp      глобальные переменные

global Fps

load('ReI1'); load('ImI1'); чтение из файлов сгенерированных токов начала и конца load('ReI2'); load('ImI2'); линии

load('ReU1'); load('ImU1'); чтение из файлов сгенерированных напряжений начала

load('ReU2'); load('ImU2'); и конца линии

i=size(ReI1,2)-5;

I=[complex(ReI1(2:4,i),ImI1(2:4,i)); complex(ReI2(2:4,i),ImI2(2:4,i))]; из сгенерированных файлов осциллограмм берём вектор тока.

x = fmincon(@CelFun,[10;1] ,[],[],[],[],[0.00001; 0.00001],[19.99; 2]); процедура минимизации. В качестве результата возвращает вектор х, состоящий из двух элементов: расстояния до места КЗ и проводимости закоротки.

Вывод

          С использованием упрощённой модели закоротки и процедуры локальной минимизации был построен алгоритм определения места повреждения.

Скачать файл