Процедура определения места повреждения на языке программирования Matlab, страница 2

5.2.3 Погонные параметры линии

Продольные погонные сопротивления

При формировании матрицы активных продольных погонных сопротивлений размерности 3x3 учитываем:

­  сопротивление земли:                            R_з = p²×f×10^-4, Ом/км

­  сопротивление фазных проводов:         R0_k,k = R_ф, Ом/км

где k – изменяется от 1 до 3 (индекс элемента матрицы, или номер провода (фазы) по порядку А, В, С).

Тогда матрица активных погонных сопротивлений будет иметь вид:

          Внешнюю индуктивность проводов будем вычислять с учетом влияния земли. Под влиянием зарядов проводов на поверхности земли будут индуцироваться заряды, поле которых можно заменить зарядами, расположенными на глубине 1000 м, это эквивалентная глубина протекания тока в грунте для средних условий при частоте 50 Гц. Таким образом, внешнее индуктивное сопротивление (Ом/км) определяется по формуле:

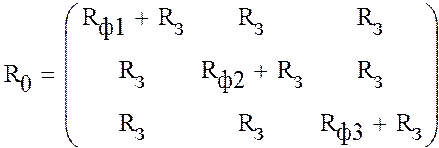
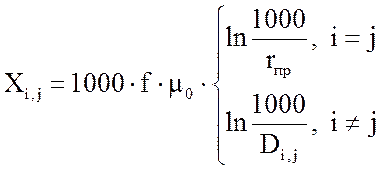          где D – матрица расстояний между фазами (рассчитана ранее), rпр – радиус проводов.

          Итак, сложив активное, как действительную часть и реактивное сопротивления, как мнимую, получаем матрицу продольных погонных сопротивлений линии: Z₀=R₀ + jX₀

Поперечные погонные проводимости

          Проводимость фазы, обусловленная потерями мощности на корону одной фазы:

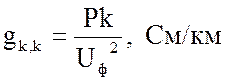где: Pk_ф=Pk/3 – погонные потери мощности на корону одной фазы, кВт; U_ф – действующее значение фазного напряжения: 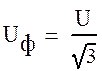, кВ

          Матрица поперечных погонных активных проводимостей, обусловленная потерями мощности на корону: G0_k,k=g_k,k, См/км

          Ёмкости C₀ рассчитаем, сформировав, а затем обратив матрицу потенциальных коэффициентов P₀:

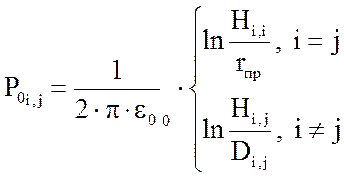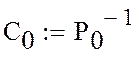, Ф/м.

Матрица поперечных погонных емкостных проводимостей:

В₀=2∙π∙f∙С₀, См/км

Итак, получаем матрицу поперечных погонных проводимостей линии: Y₀=G₀+jB₀,  действительная составляющая учитывает потери энергии на корону проводов, а мнимая – емкость проводов.

          Приведём текст процедуры для расчёта погонных параметров линии.

function [Z0, Y0] = Pogon_Par(X1, Y1, F, Pk, U, f_nom, r)

g0=0.029^-1;             Проводимость материала проводов

eps0=1/(36e9*pi);      Диэлектрическая проницаемость воздуха

mu0=4e-7*pi;            Магнитная проницаемость ваккумавакуумаостоянная

Uf=U/sqrt(3);             Фазное напряжение

Rf=1e3/(g0*F);          Активное сопротивление проводов

R3=pi^2*1e-4*f_nom;         Сопротивление земли

R0=zeros(3,3);           Обнуляем матрицу погонных активных сопротивлений

form=1:3

R0(m,m)=Rf;    На места диагональных элементов матрицы R0 ставим сопротивление проводов

G0(m,m)=Pk*10^-3/(3*Uf^2); Рассчитываем диагональные элементы матрицы G0 (матрица продольных проводимостей, учитывающих потери на корону)

forn=1:3

R0(m,n)=R0(m,n)+R3; Недиагональные элементы матрицы R0

H(m,n)=sqrt((X1(m)-X1(n))^2+(Y1(m)+Y1(n))^2); Матрица расстояний между проводами и ими же, зеркально отображёнными относительно поверхности земли

D(m,n)=sqrt((X1(m)-X1(n))^2+(Y1(m)-Y1(n))^2); Матрица расстояний между фазами

if (m==n)

X0(m,n)=1e3*f_nom*mu0*log(1000/r); Внешняя индуктивность проводов с учётом влияния земли.

P0(m,n)=(1e3*log(H(m,m)/r))/(2*pi*eps0); матрица потенциальных коэффициентов, необходимая для расчёта матрицы поперечных погонных ёмкостных проводимостей

elseif (m~=n)

X0(m,n)=1e3*f_nom*mu0*log(1000/D(m,n));

P0(m,n)=(1e3*log(H(m,n)/D(m,n)))/(2*pi*eps0);

end

end

end

B0=2*pi*f_nom*P0^-1; матрица поперечных погонных ёмкостных проводимостей

Z0=[R0+X0*sqrt(-1)]; матрица погонных сопротивлений

Y0=[G0+B0*sqrt(-1)]; матрица погонных проводимостей

5.3. Имитация повреждения

          В данной работе в расчётах Повреждение имитируется единственной проводимостью – проводимостью закоротки Y_КЗ (включением в точку замыкания трёхфазного однополюсника). В общем случае матрица Y_КЗ симметрична, а значит имеет шесть элементов, подлежащих оценке. Она имеет следующую структуру:

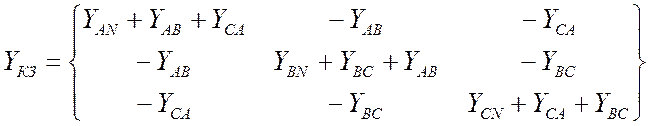          где Y_AN – проводимость между фазой А и землёй, Y_ВN – проводимость между фазой В и землёй, Y_СN – проводимость между фазой С и землёй; Y_AВ, Y_ВС, Y_СА – междуфазные проводимости, имитирующие повреждения. Все переходные сопротивления примем одинаковыми.

          При таком задании проводимости закоротки задача ОМП сводится к поиску минимума функции по двум переменным: расстоянию до места повреждения и проводимости закоротки. В качестве третьей переменной можно рассматривать тип повреждения (его номер), который можно определить путём перебора всех его значений (от 1 до 11), будем считать, что имеет место тот тип повреждения, при котором достигается минимум целевой функции.

 

5.4. Расчёт токов по концам линии