


Функции случайных величин.
h1=x1+x2 h1=x1x2
у=х1+х2 у=х1х2
Пусть имеется произвольное вероятностное пространство (Е,U,Р), функция x(w), где wÎЕ – случайная величина, определенная на вероятностном пространстве (x(w)) и функция у=g(х) – функция определения на всей вещественной оси.
Определение 1. Суперпозиция h=j(x) случайной величины x, определенной на вероятностном пространстве x(w), wÎЕ и обычной функции j(х)=у, определенной на всей вещественной оси, называется функцией случайной величины x, если "хÎR событие (h<х)ÎU (алгебре событий).
Если имеется n произвольных случайных величин x1, x2, …, xn, определенных на одном и том же вероятностном пространстве и какая-то функция Z=f(х1, …,хn), то можно рассматривать случайную величину
z=f(x1, x2, …, xn), (1)
где z связана с x1, x2, …, xn функциональной зависимостью.
Например, Z=ехр (х1+2х2×х3)
z=ехр (x1+2x2×x3).
Поскольку
законы распределения случайной величины xi, ![]() известны, то и
законы распределения случайной величины h (или z) также известны.
известны, то и
законы распределения случайной величины h (или z) также известны.
h=g(x), y=g(x), Fx(x)=P(x<x)
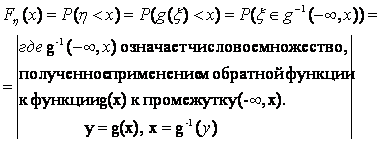
Плотность
распределения ![]() .
.
Если
известна Рh(х), то 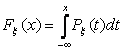 .
.
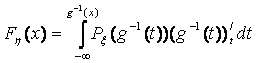 (2)
(2)
Эта функция дает возможность по известной плотности распределения записать функцию распределения. Формула (2) может быть получена с помощью теоремы.
Теорема 1 (о законе распределений функций от случайной
величины). Пусть есть случайный вектор ![]() т.е.
т.е.
![]() - вектор функция, где
- вектор функция, где ![]() - вектор с непрерывными компонентами
и
- вектор с непрерывными компонентами
и ![]() - плотность распределения вектора
- плотность распределения вектора ![]() .
.
Если отображение ![]() непрерывно
и дифф-мо и его якобиан
непрерывно
и дифф-мо и его якобиан ![]() , то тогда
случайный вектор
, то тогда
случайный вектор ![]() имеет непрерывное
распределение, плотность которого:
имеет непрерывное
распределение, плотность которого:
![]() (3)
(3)
![]() y1=g1(x1, …, xr) Точка
M(x1, …, xr)
y1=g1(x1, …, xr) Точка
M(x1, …, xr)
………………
yr=gr(x1,
…, xr) Точка ![]() (y1,
…, yr)
(y1,
…, yr)
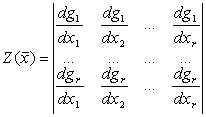 - якобиан преобразования.
- якобиан преобразования.
(Без доказательства).
Теорема 2 (при h=Аx+В, А¹0, у=Ах+В). Если случайная величина x распределенная по нормальному закону с математическим ожиданием М[x]=m и дисперсией D[x]=s2, то случайная величина h, связанная с ней линейной функцией h=Аx+В, А¹0, также имеет нормальный закон распределения, причем
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.