
49
Уравнения состояния ,внутренняя энергия идеального и реального невырожденных газов.Уравнение Ван-дер-Ваальса.
Уравнения состояния.
Состояние заданной массы газа определяется значением 3-х параметров P,V,T. Эти параметры закономерно связаны др.с др., так что изменение одного одного влечет за собой изменение других.Соотношение определяет связь между параметрами какого-либо тела наз. уравнением состояния этого тела.Простым объектом, для которого может быть рассмотрено уравнение состояние является идеальный газ.Идеальным газом наз. газ, молекулы которого имеют принебрежимо малый собственный объем и невзаимодействуют др. с др. на расстоянии.
![]() (1) –
это уравнение состояния идеального газа.
(1) –
это уравнение состояния идеального газа.
Для данной массы идеального газа отношение произведения P*V к температуре T есть величина постоянная.
Закон Авогадро: моль любого вещества в газообразном состоянии при одинаковой температуре и давлении занимает один и тот же объем.В частности при нормальных условиях t=0C и P=105 Па, V=22,4 гр/ моль .Отсюда следует, что в случае, когда количество газа =1 молю,величина const (1) будет одинакова для всех газов .Обозначим эту const через R и
Напишем уравнение состояния идеального газа следующем образом :PVm=RT, (2) где Vm- объем одного моля газа, R=8,31 Дж/моль *К – газовая постоянная .
Чтобы получить уравнение
состояния для произвольной массы идеального газа умножим обе части уравнения
(2) на m/m, m- молярная масса газа![]() , т. к.
, т. к. ![]() (3)
(3)
Умножив и разделив правую часть (3) N A: PV=nNAKT, где К =R/Na=1,38 *10-23 Дж /К – постоянная БольцманаÞRV= NkT разделим на V, где N=nNl, число молекул ,содержащихся в массе газа, а n =N/V –число молекул в единицу объема.
P=nkT (4).
Внутренняя энергия идеального газа представляет собой кинетическую энергию его молекул.
Для одного моля Um=![]() NA=i/2*RT Moлекулу одноатомного газа можно рассмотреть как
материальную точку, потому что практически вся масса такой частицы
сосредоточена в атомном ядре. Такая молекула имеет три степени свободы
постоянного движения Þ Um=3/2*m/m*RT. Внутреннею
энергию произвольной массы одноатомного идеального газа с молярной массой m
определяется по ф-ле:
NA=i/2*RT Moлекулу одноатомного газа можно рассмотреть как
материальную точку, потому что практически вся масса такой частицы
сосредоточена в атомном ядре. Такая молекула имеет три степени свободы
постоянного движения Þ Um=3/2*m/m*RT. Внутреннею
энергию произвольной массы одноатомного идеального газа с молярной массой m
определяется по ф-ле:![]()
Внутренняя энергия реального
газа равна сумме кинетической энергии хаотического движения молекул и их
взаимной потенциальной энергии:U=Wk+Wп
Кинетическая энергия для моля реального газа совпадает с кинетической энергией
для моля соответствующего идеального газа ![]() ,СV-молярная
теплоемкость газа. Взаимная потенциальная энергия обусловлена силами
межмолекулярного взаимодействия зависящими от расстояния между молекулами.
Потенциальная энергия зависит от среднего расстояния между молекулами то есть
от удельного объема газа и от характера межмолекулярного взаимодействия U=CVT+Wn Wn=
-a/V
,СV-молярная
теплоемкость газа. Взаимная потенциальная энергия обусловлена силами
межмолекулярного взаимодействия зависящими от расстояния между молекулами.
Потенциальная энергия зависит от среднего расстояния между молекулами то есть
от удельного объема газа и от характера межмолекулярного взаимодействия U=CVT+Wn Wn=
-a/V
Уравнение Вандер-Вальса : Для
описания поведения реальных газов было предложено много различных уравнений.
Самым простым и в то же время дающим достаточно хорошие результаты оказывает
уравнение, предлагаемое Вандер-Вальсом в 1873 г. Это ур-ие было получено путем
внесения поправок в ур-ие (2) и имеет вид![]() -для
одного моля. Р -давление, оказываемое на газ извне, а и b – постоянные
Вандер-Вальса имеющие для разных газов различные значения. Поправка a/Vm2
характеризует к внешнему давлению, обусловленную взаимодействиями между
молекулами. Из-за притяжения молекул друг другу газ сжимает сам себя. Если бы
взаимодействие между молекулами вдруг прекратилось, то для того чтобы удержать
газ в приделах того или иного объема, понадобилось бы увеличить внешнее давление
на величину а/vm2.
В следствии быстрого уменьшения сил притяжения между молекулами с увеличением
расстояния между ними заметные воздействия молекул друг на друга
осуществляется в пределах небольших расстояний, наз. радиусом молекулярного
взаимодействия. Представим себе в газе воображаемую плоскость. Молекулы ,
находящиеся по обе стороны от плоскости в слоях толщиной радиуса молекулярного
взаимодействия, притягивают друг друга с силой пропорционально как числу
молекул в одном слое, так и числу молекул в другом слое. Оба числа
пропорциональны количеству молекул в единице объёма п, которое в свою
очередь обратно пропорциональна объёму газа. Т. о. давление оказывается прмо
пропорциональна п2 или обратно пропорциональна V2. Поправка к объёму b характеризует ту часть объёма сосуда, которая не
доступна для движения молекул. Т.е. b это есть поправка собственного
объёма. Уравнение для произвольного количества молей
-для
одного моля. Р -давление, оказываемое на газ извне, а и b – постоянные
Вандер-Вальса имеющие для разных газов различные значения. Поправка a/Vm2
характеризует к внешнему давлению, обусловленную взаимодействиями между
молекулами. Из-за притяжения молекул друг другу газ сжимает сам себя. Если бы
взаимодействие между молекулами вдруг прекратилось, то для того чтобы удержать
газ в приделах того или иного объема, понадобилось бы увеличить внешнее давление
на величину а/vm2.
В следствии быстрого уменьшения сил притяжения между молекулами с увеличением
расстояния между ними заметные воздействия молекул друг на друга
осуществляется в пределах небольших расстояний, наз. радиусом молекулярного
взаимодействия. Представим себе в газе воображаемую плоскость. Молекулы ,
находящиеся по обе стороны от плоскости в слоях толщиной радиуса молекулярного
взаимодействия, притягивают друг друга с силой пропорционально как числу
молекул в одном слое, так и числу молекул в другом слое. Оба числа
пропорциональны количеству молекул в единице объёма п, которое в свою
очередь обратно пропорциональна объёму газа. Т. о. давление оказывается прмо
пропорциональна п2 или обратно пропорциональна V2. Поправка к объёму b характеризует ту часть объёма сосуда, которая не
доступна для движения молекул. Т.е. b это есть поправка собственного
объёма. Уравнение для произвольного количества молей ![]()
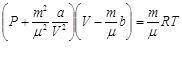
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.