21
Максвелл
на основе полученных им уравнений электромагнетизма предсказал существования
ЭМВ. Покажем, что в однородной изотропной непроводящей среде (![]() ) векторы поля удовлетворяют волновому
уравнению, причем скорость распространения
) векторы поля удовлетворяют волновому
уравнению, причем скорость распространения 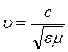 , где
, где 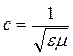 . Выпишем систему уравнений Максвелла:
. Выпишем систему уравнений Максвелла: 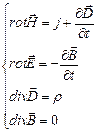 (1). В однородной изотропной среде
(1). В однородной изотропной среде ![]() , а из условия
, а из условия ![]() (поскольку
(поскольку
![]() ) следовательно, что
) следовательно, что ![]() . Из закона сохранения заряда
. Из закона сохранения заряда ![]() вытекает , что
вытекает , что ![]() , то
есть
, то
есть ![]() . Но независящее от времени распределение
плотности заряда можно породить только постоянное поле, а если нас интересует
переменное поле, то можно считать, что
. Но независящее от времени распределение
плотности заряда можно породить только постоянное поле, а если нас интересует
переменное поле, то можно считать, что ![]() . Это
позволяет записать систему уравнений Максвелла в виде:
. Это
позволяет записать систему уравнений Максвелла в виде: 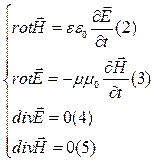 Дифференцируя
уравнение (2) по времени и заменяя в полученном уравнении
Дифференцируя
уравнение (2) по времени и заменяя в полученном уравнении ![]() из уравнения (3), имеем:
из уравнения (3), имеем: 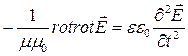 (6). Пользуясь формулой векторного
анализа
(6). Пользуясь формулой векторного
анализа ![]() и принимая во внимание (4), получим:
и принимая во внимание (4), получим: 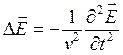 (7). Аналогично из (2) и (3) находим:
(7). Аналогично из (2) и (3) находим: 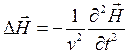 (8). (7) и (8) – это волновые
уравнения соответственно для векторов
(8). (7) и (8) – это волновые
уравнения соответственно для векторов ![]() и
и ![]() удовлетворяет волновому уравнению,
вытекает, что ЭМП, которое характеризуют эти векторы, может распространяться в
виде волны. Скорость распространения ЭМВ
удовлетворяет волновому уравнению,
вытекает, что ЭМП, которое характеризуют эти векторы, может распространяться в
виде волны. Скорость распространения ЭМВ 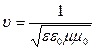 определяется
исключительно свойствами среды. Рассмотрим теперь решение волнового уравнения.
Начнем с самого простого случая пространственного одномерного волнового
уравнения:
определяется
исключительно свойствами среды. Рассмотрим теперь решение волнового уравнения.
Начнем с самого простого случая пространственного одномерного волнового
уравнения: ![]() (9). Общие решение этого уравнения имеет
вид:
(9). Общие решение этого уравнения имеет
вид:![]() (10). Если в момент времени равным нулю
изобразить функцию
(10). Если в момент времени равным нулю
изобразить функцию ![]() и
и ![]() то в
последующие моменты времени эти функции смещаются вдоль оси
то в
последующие моменты времени эти функции смещаются вдоль оси ![]() со скоростью
со скоростью ![]() как
целое:
как
целое: ![]() -вправо,
-вправо, ![]() -влево.
Ограничимся так называемыми гармоническими монохроматическими волнами, то есть
синусоидальными волнами с одной циклической частотой
-влево.
Ограничимся так называемыми гармоническими монохроматическими волнами, то есть
синусоидальными волнами с одной циклической частотой ![]() .
Гармоническая зависимость любой величины S от времени
может быть представлена в общем в виде:
.
Гармоническая зависимость любой величины S от времени
может быть представлена в общем в виде: ![]() , где S0 – значение рассматриваемой величины в точке с координатой x в момент времени
равное нулю. Решение уравнение (8) и удовлетворяющее условию (10), дающее
гармоническая зависимость S от t имеет вид:
, где S0 – значение рассматриваемой величины в точке с координатой x в момент времени
равное нулю. Решение уравнение (8) и удовлетворяющее условию (10), дающее
гармоническая зависимость S от t имеет вид: ![]() (11). Фазы волны,
то есть ее состояние в данной точке пространства в данный момент времени
определяется выражением
(11). Фазы волны,
то есть ее состояние в данной точке пространства в данный момент времени
определяется выражением ![]() . Нам понадобиться еще
выражение для плоской волны, распространяющейся в произвольном направлении, с
постоянным вектором m. Поскольку уравнение пространства, перпендикулярной
вектору m. Имеет вид:
. Нам понадобиться еще
выражение для плоской волны, распространяющейся в произвольном направлении, с
постоянным вектором m. Поскольку уравнение пространства, перпендикулярной
вектору m. Имеет вид: ![]() , плоскую волну можно записать в виде:
, плоскую волну можно записать в виде: ![]() (12). Введем волновой вектор
(12). Введем волновой вектор ![]() , определив его как:
, определив его как: ![]() ,
, ![]() -
единичный вектор в направлении распространения волны. Следовательно,
-
единичный вектор в направлении распространения волны. Следовательно, ![]() (13). Убедимся , что (14) –решение
пространственного трехмерного волнового уравнения.
(13). Убедимся , что (14) –решение
пространственного трехмерного волнового уравнения.
Удобно
ввести оператор Даламбера, ð![]() (14)
(14)
Где D- оператор Лапласа. Следовательно волновое уравнение для скалярной величины
ðS=0 (15)
применяя к (13) оператор ð, получим
ðS(r,t)=![]()
 вектор
вектор
![]() называется волновым вектором потому, что
имеет непосредственное отношение к длине волны. Длиной волны называют
расстояние между двумя ближайшими точками волны, обладающими одинаковой фазой.
Рассмотрим плоскую волну 13 и допустим, что фазы в точках r и r+l, одинаковы. Тогда в любой момент времени должно
соблюдаться равенство:
называется волновым вектором потому, что
имеет непосредственное отношение к длине волны. Длиной волны называют
расстояние между двумя ближайшими точками волны, обладающими одинаковой фазой.
Рассмотрим плоскую волну 13 и допустим, что фазы в точках r и r+l, одинаковы. Тогда в любой момент времени должно
соблюдаться равенство: ![]() . Это может быть лишь в
том случае если
. Это может быть лишь в
том случае если ![]() или
или ![]() .
Если представить пространственно-временное изменение векторов
.
Если представить пространственно-временное изменение векторов ![]() и
и ![]() в виде
плоских волн:
в виде
плоских волн: ![]() (16), то эти выражения
безусловно удовлетворяют выражениям (7) и (8). Однако, чтобы они удовлетворяли
уравнениям Максвелла, на них следует наложить еще дополнительные условия.
Подставляя их соответственно в (4) и (5) получим
(16), то эти выражения
безусловно удовлетворяют выражениям (7) и (8). Однако, чтобы они удовлетворяли
уравнениям Максвелла, на них следует наложить еще дополнительные условия.
Подставляя их соответственно в (4) и (5) получим ![]() ,
, ![]() . Равенство нулю означает, что
. Равенство нулю означает, что ![]() и
и ![]() . Кроме
того, нетрудно установить, что
. Кроме
того, нетрудно установить, что ![]() и
и ![]() взаимно
взаимно ![]() . Чтобы
убедиться в этом представим (16) в левые части (2) и (3):
. Чтобы
убедиться в этом представим (16) в левые части (2) и (3): ![]() и
и ![]() .
Следовательно, уравнения (2) и (3) примут вид:
.
Следовательно, уравнения (2) и (3) примут вид: ![]() или
или 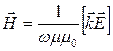 (17),
(17), ![]() или
или 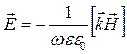 (18). Достаточно умножить на
(18). Достаточно умножить на ![]() или
(18) на
или
(18) на ![]() , чтобы получить:
, чтобы получить: ![]() (19).
Следовательно векторы
(19).
Следовательно векторы ![]() ,
, ![]() ,
, ![]() взаимно
взаимно ![]() и образуют
правую тройку векторов. Вектор
и образуют
правую тройку векторов. Вектор ![]() определяет направление
распространение волны. Векторы
определяет направление
распространение волны. Векторы ![]() и
и ![]() колеблются в плоскости,
колеблются в плоскости, ![]() направлению
направлению ![]() . Таким
образом ЭМВ в указанных условиях является поперечно - поляризованной
(направление колебаний
. Таким
образом ЭМВ в указанных условиях является поперечно - поляризованной
(направление колебаний ![]() направлению распространения). Если
ввести четырехмерный волновой вектор кванта света фотона
направлению распространения). Если
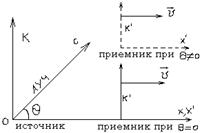
ввести четырехмерный волновой вектор кванта света фотона ![]() то легко получить формулы, описывающие
эффект Доплера; он обнаруживается для волн любой природы и заключается в том,
что при относительном движении источника и приемника (наблюдателя) частота
света или звука, определяемая наблюдателем отличается от частоты, измеренной в
СО где источник покоится. Рассмотрим плоскую световую волну, наблюдаемую в
системе отсчета
то легко получить формулы, описывающие
эффект Доплера; он обнаруживается для волн любой природы и заключается в том,
что при относительном движении источника и приемника (наблюдателя) частота
света или звука, определяемая наблюдателем отличается от частоты, измеренной в
СО где источник покоится. Рассмотрим плоскую световую волну, наблюдаемую в
системе отсчета ![]() и характеризуемым четырех мерным
вектором
и характеризуемым четырех мерным
вектором ![]() . Выберем систему
. Выберем систему ![]() так
чтобы луч света распространялся в этой системе в пространстве
так
чтобы луч света распространялся в этой системе в пространстве![]() и составляет угол q
с осью
и составляет угол q
с осью ![]() . Выпишем компоненты четырех
. Выпишем компоненты четырех
мерного
вектора ![]() ;
; ![]() ,
, ![]() ,
,![]() компоненты
компоненты ![]() в системе К находятся по формулам:
в системе К находятся по формулам: ![]() ,
, ![]() ,
, ![]() или для
или для ![]() :
:
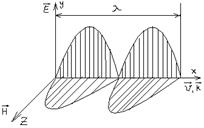
![]() (20), следовательно, если
в системе
(20), следовательно, если
в системе ![]() частота света была равной
частота света была равной ![]() , то в системе К она уже будет согласно
(20) иной. Для
, то в системе К она уже будет согласно
(20) иной. Для ![]() :
:
![]() если принять во внимание (20), то
если принять во внимание (20), то ![]() (21) пусть источник покоится в системе
(21) пусть источник покоится в системе ![]() , тогда приборы, покоящиеся в системе,
фиксируют собственную частоту источника света
, тогда приборы, покоящиеся в системе,
фиксируют собственную частоту источника света ![]() ,
найдем зависимость частоты wв системе К от угла Q.
Из (21) следует, что
,
найдем зависимость частоты wв системе К от угла Q.
Из (21) следует, что ![]() откуда
откуда 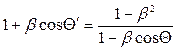 и
следовательно (20) может окончательно записаться так
и
следовательно (20) может окончательно записаться так 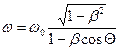 эта
формула описывает эффект Доплера. Наблюдатель в системе К зафиксирует частоту
излучения w, не совпадающую с собственной частотой w0.
эта
формула описывает эффект Доплера. Наблюдатель в системе К зафиксирует частоту
излучения w, не совпадающую с собственной частотой w0.
1.
Если излучение принимается в направлении относительной скорости
следовательно продольный эффект Доплера. Если к системе отсчета ![]() то источник удаляется от наблюдателя и
свет движется
то источник удаляется от наблюдателя и
свет движется
в
направлении, противоположном направлению оси. Тогда Q=p
и cosQ=-1
следовательно ![]() и
и ![]() снижение
частоты.
снижение
частоты.
2.
если система ![]() находится слева от К, то cosQ=-1 и источник
приближается к наблюдателю
находится слева от К, то cosQ=-1 и источник
приближается к наблюдателю
![]()
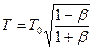 (w>w0). Если источник движется
перпендикулярно лучу зрения
(w>w0). Если источник движется
перпендикулярно лучу зрения ![]() следовательно попереч
эффект Доплера:
следовательно попереч
эффект Доплера: ![]() Э.Д. позволяет измерять
скорость движения источников излучения или рассеивающих волны объектов и
находит широкое практическое применение. Так в астрофизике Э.Д. используется
для определения спектра излучений далеких галактик. Используется для
измерения скорости движ. целей.
Э.Д. позволяет измерять
скорость движения источников излучения или рассеивающих волны объектов и
находит широкое практическое применение. Так в астрофизике Э.Д. используется
для определения спектра излучений далеких галактик. Используется для
измерения скорости движ. целей.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.