Определение электрохимического эквивалента вещества, заряда иона и числа Фарадея: Методическое пособие к лабораторной работе № 8, страница 2

В действительности процесс диссоциации носит более слож-ный характер, так как возникающие ионы взаимодействуют с мо-лекулами воды. Например, в случае водного раствора ион  Н⁺ не остаётся в свободном состоянии (свободный протон), а соединяе-тся с молекулой воды, образуя молекулярный положительный ион  Н₃О⁺  (ион гидроксония), при растворении медных солей об-разуются группы  Cu(H₂O)₄⁺⁺  и т.д.. Такие процессы называются гидратацией, если в качестве растворителя выступает вода, или в общем случае – сольватацией.

Итак, полярные молекулы диссоциируют в растворе под влиянием полярных молекул растворителя. Степень диссоциации зависит от природы молекул как растворённого вещества так и растворителя. Имеется параллелизм между диэлектрической проницаемостью вещества и его способностью вызывать диссо-циацию: чем больше диэлектрическая проницаемость раствори-теля, тем большуу степень диссоциации он вызывает. Вода зани-мает исключительное место среди растворителей, являясь лучшим растворителем электролитов. Остальные растворители, особенно органические, плохо растворяют электролиты. Для сравнения ниже приводятся значения относительной диэлектрической проницаемости для наиболее широко применя-емых растворителей:

1.  Цианисто-водородная кислота ………96

2.  Вода ……………………………………80

3.  Муравьиная кислота ………………….62

4.  Этиловый спирт ……………………….25

5.  Диэтиловый эфир ……………………..4,1

6.  Бензол ………………………………….2,3

§ 2. Закон разведения Оствальда

Для количественной характеристики степени диссоциации вводится в рассмотрение коэффициент диссоциации  α.

Предположим, что в единице объёма раствора имеется  n_o  молекул растворённого вещества, из которых  n^/ _o= αn_o  диссоции-рованы на ионы, а  n^//_o= n_o - αn_o=(1-α)n_o  не диссоциированы. Коэффициент диссоциации  α  указывает степень диссоциации молекул в растворе. Очевидно, что если  α = 1 , то все молекулы диссоциированы, а если  α = 0 , то диссоциация отсутствует. По данной степени диссоциации раствора мы имеем дело с подвиж-ным (динамическим) равновесием, при котором число элементар-ных актов диссоциации в единицу времени равно числу актов ре-комбинации.

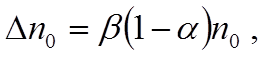Число новых пар ионов, возникающих в единицу времени в единице объёма, пропорционально числу наличных молекул, следовательно

где  β – коэффициент пропорциональности.

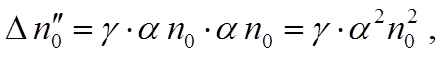Число ионов, воссоединяющихся в молекулы, пропорциона-льно как числу положительных, так и числу отрицательных ионов. Так как число ионов каждого знака в единице объёма рав-но  αn_o  то, следовательно, число пар ионов, воссоединяющихся в единице объёма в единицу времени можно считать равным

где  - коэффициент пропорциональности.

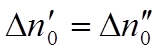Условие равновесия между процессом диссоциации и процессом рекомбинации, очевидно, сводится к тому, чтобы чис-ло вновь образующихся пар ионов равнялось числу воссоединяю-щихся пар ионов, т.е. чтобы

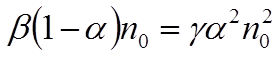или

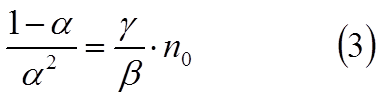Из последнего равенства находим

Полученная формула выражает закон Оствальда, показыва-ющий как зависит коэффициент диссоциации α от концентрации раствора  n_o. Отношение коэффициентов  α / β  не зависит от  n_o, а зависит от природы раствора и тех условий (температуры), при которых он находится.

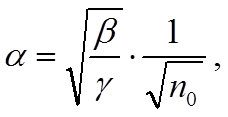Формула  (3)  позволяет сделать некоторые выводы о степени диссоциации молекул в растворе. Если раствор слабый, т.е.  n_o=0 то  α  близко к единице, что означает – практически все молекулы растворённого вещества диссоциированы. Если предположить, что степень диссоциации мала, то в равенстве  (3)  можно пренеб-речь в числителе коэффициентом  α  по сравнению с единицей, тогда получим