Экспериментальное определение критериев Рейнольдса, соответствующих режимам движения жидкости

        Цель работы: визуальное наблюдение двух устойчивых, качественно различных режимов движения жидкости и экспериментальное определение критериев Рейнольдса, соответствующих этим режимам движения.

       Теоретическая часть: При протекании жидкости по трубам и каналам могут иметь место два различных по своему характеру режима движения: ламинарный и турбулентный.

    Ламинарный – такой режим, при котором поток жидкости движется отдельными струйками или слоями и траектории отдельных частиц не пересекаются между собой, линии тока совпадают с траекторией частиц.

    Турбулентный – такой режим, при котором частицы жидкости перемещаются, и траектории отдельных частиц представляют собой сложные линии, пересекающиеся между собой.

Наличие ламинарного и турбулентного режима зависит от скорости движения, вязкости жидкости, и геометрических размеров живого сечения потока.

    Скорость, при которой происходит смена режимов движения, называется критической скоростью. При этом различают две критические скорости: нижнюю и верхнюю. При нижней критической скорости турбулентное движение переходит в ламинарное. При верхней критической скорости ламинарное движение переходит  в турбулентное.

    Ход работы:

По измеренной температуре воды в напорном баке определяем кинематический коэффициент воды:

ν =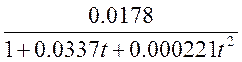 ,   где t-температура воды.                                                                    (1)

По измеренному объему воды, поступившей в мерный бак, подсчитывается для каждого опыта расход воды:

Q=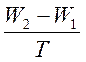                                                                                                                                            (2)

Здесь  и  объем воды в мерном баке соответственно начальный и конечный.

Средняя скорость течения воды:  v=                                                                                             (3)

Скорость, при которой произойдет смена режимов движения жидкости, и будет критической скоростью  υкр.

По формуле  Re=                                                                                                                           (4)

 для каждого опыта по найденным значениям подсчитывается число Re.

Значение Re  соответствующее критической скорости движения υкр ,является критическим числом Рейнольдса.

    Обработку данных занести в таблицу.