Исследование системы временной коммутации на примере модели системы массового обслуживания с очередями

ИССЛЕДОВАНИЕ СИСТКЕМЫ ВРЕМЕННОЙ КОММУТАЦИИ НА ПРИМЕРЕ МОДЕЛИ СИСТЕМЫ МАССОВОГО ОБСЛУЖИВАНИЯ С ОЧЕРЕДЯМИ

Система уравнений Эрланга для СМО с очередями

            В отличие от СМО   с отказами, если   все каналы заняты, то запрос не получает отказа , а становится в очередь.

n - число каналов;

Пусть  N (t) – число запросов, находящихся  в данный момент времени  t  в системе и обслуживаемых коммутатором;  N (t) - случайный процесс с конечным множеством значений и непрерывным временем.

p_k(t) = P{N(t) = k} - вероятность того , что в момент времени t в системе находится ровно k заявок, т.е. p_k(t)  - одномерные законы распределения процесса N(t)  .

Число k может принимать значения 0,1,2, . . . ,n, n+1, . . .  .

Если n ³ k ,это означает , что в СМО k каналов занято и очереди нет , если k > n , то все каналы заняты обслуживанием  и k-n заявок стоят в очереди .

Для составления дифференциальных уравнений Колмогорова - Чемпена плотности перехода, т.е. веса ребер направленного графа l_ij , i ¹ j имеют вид:

         l_{i i-1}=im  при i=1,2,...,n ;

         l_{i i-1}=nm  при i>n ;

         l_{i i+1}=l  при i=0,1,...

         l_{i i ±k}=0  при k ³ 2

            Следовательно, система уравнений Колмогорова - Чепмена имеет вид:

p₀'(t)=mp₁(t)-lp₀(t) ;

p₁'(t)=lp₀(t)+2mp₂(t)-(l+m)p₁(t) ;

. . .

p_i'(t)=lp_i-1(t)+(i+1)mp_i+1(t)-(l+im)p_i(t) , i=1,2,...,n-1 ;

. . .

p_n'(t)=lp_n-1(t)+nmp_n+1(t)-(l+nm)p_n(t) ;

. . .

p_k'(t)=lp_k-1(t)+nmp_k+1(t)-(l+nm)p_k(t) , k=n,n+1,..

и называется системой дифференциальных уравнений Эрланга для СМО с очередями.

            Если в начальный момент времени заявок в СМО нет: p_k(0)=1, k=0;   p_k(0)=0 , k>0,  то система уравнений Эрланга имеет единственное решение, однако в общем случае записать это решение практически невозможно.

            Наиболее важным частным случаем решения системы уравнений Эрланга является ее решение в стационарном режиме, т.е. когда существуют конечные пределы  p_k = lim p_k(t) = 0.

Следовательно, система дифференциальных уравнений Эрланга превратится в систему линейных алгебраических уравнений для отыскания вероятностей p_k :

0=mp₁-lp₀ ;

0=lp₀+2mp₂-(l+m)p₁ ;

. . .

0=lp_i-1+(i+1)mp₁₊₁-(l+im)p_i  ,i=1,2,...,n-1 ;

. . .

0=lp_n-1+nmp_n+1-(l+nm)p_n ;

. . .

0=lp_k-1+nmp_k+1-(l+nm)p_k , k=n,n+1,...

Кроме того, на вероятности p_k  налагается естественное условие нормировки :.            Рекуррентно решая систему, получим для вероятностей рк формулу, которая называется формулой Эрланга для истемы с очередями

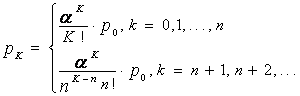
 и определим p₀ из условия нормировки :

 å^¥ p_k= åⁿ (a^k/k!)p₀ + å^¥(a^k/n^k-nn!)p₀ =p₀[  åⁿ(a^k/k!) + (nⁿ/n!)å^¥(a/n)^k ] = 1.

^{k=0              k=0                          k=n+1                                          k=0                                    k=n+1}