Исследование системы временной коммутации на примере модели системы массового обслуживания с очередями, страница 2

Условие нормировки удовлетворяется только в том случае, если ряд в левой части послед-него равенства сходится. Этот ряд является геометрическим рядом и сходится, если a/n <1 ,

т.е. a<n . В этом случае: å^¥  (a/s)^k  = (a/n)ⁿ⁺¹/(1-a/n) ,

                                  ^k=n+1

откуда     .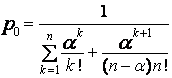

            Если a/n ³ 1 , то геометрический ряд расходится и стационарного режима в СМО не существует , так как число заявок в очереди неограниченно возрастает .

            Множитель a = l/m , где   l- плотность входного потока, m - интенсивность обслуживания,  называется   плотностью  нагрузки СМО  и имеет смысл среднего числа заявок, поступающих в  СМО  за среднее время обслуживания одной заявки.

            Формула Эрланга получена в предположении, что на вход СМО действует пуассоновский входной поток, а время обслуживания заявок распределено по показательному закону.

Основные формулы Эрланга для СМО с очередями

            Основные важные характеристики СМО с очередями, получаемые на основе формулы Эрланга, в литературе называются основными формулами Эрланга и сведены в таблицу 1.

Таблица 1.