Задания выполнить и представить результат в распечатанном и электронном виде до 7.02.06. В заголовке указать контрольная работа №2 по резервированию, наименование группы, Ф.И.О. без сокращения, в конце подпись и дату. Ниже приведены варианты контрольных работ.
1. Оцените вероятность работоспособного состояния системы, представленной тремя группами элементов: смешанным соединением элементов (мостиковая схема из пяти элементов) вторая группа из четырёх элементов. Вторая группа элементов 6, 7, 8, 9 работоспособна только тогда, когда исправны не менее двух любых элементов. Третью группу представляет один элемент. P1=0.9, P2=0.9, P3=0.95, P4=0.95, P5=0.9; Р6=Р7=Р8=Р9=0.9. Р10 = 0.95. Пояснить расчётом, как изменится структура второй группы элементов, чтобы её надёжность (в.б.р.) была не ниже 0.95. Провести вычисление надёжности системы с помощью общего резервирования. Рзад=0.95.
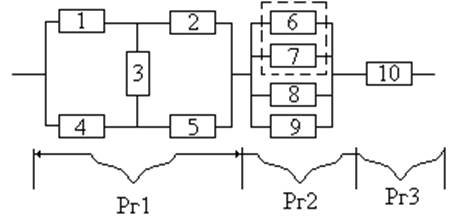
2. Привести расчёт надёжности в случае общего «горячего» резерва в период нормальной эксплуатации (период «зрелости») для следующей структурной схемы:
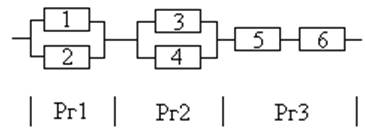
Расчёт выполнить для времени t=1000ч. Первая группа элементов (Рг1) 1 и 2 с зависимой интенсивностью отказов: l1=2*10-3, l2=3*10-2, l12=3*10-3, l21=5*10-2 [ч-1]. Элементы второй группы с независимой интенсивностью отказов имеют следующие вероятности безотказной работы: Р3=0.9, Р4=0.92. Третья группа элементов: Р5=0.95 и Р6=0.9. Рзад=0.95.
3. Задача. Дана система из одного основного и двух резервных элементов, находящихся в нагруженном режиме. Имеет место нормальный закон распределения времени работы до отказа:
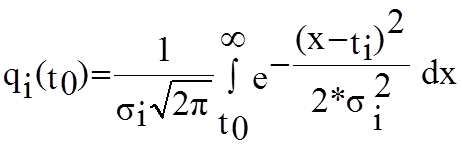
с параметрами T1=1000ч. , s1=10ч.;T2=1500ч., s2 = 15ч.; T3=1000ч. , s3 = 20ч.
Найти вероятность безотказной работы резервированной системы в течение 500 ч., вычислить среднее время работы до отказа и частоту отказов. Выполнить расчёты по резервированию в случае экспоненциального закона распределения для Р1=0.9 и Рзад-0.95. Оценить также коэффициент повышения надёжности за счёт резервирования.
4. Пояснить, что такое коэффициент выигрыша надежности или коэффициент повышения надёжности? Привести пример определения этого коэффициента в случае общего «горячего» резерва n-элементов. Пусть основная цепь элементов имеет кратность резервирования равной нулю.
5. Задача. Радиопередатчик имеет интенсивность отказов λ0=0,4*10-3 1/час. Его дублирует такой же передатчик, находящийся до отказа основного передатчика в режиме ожидания (в режиме облегченного резерва). В этом режиме интенсивность отказов передатчика λ1=0,06*10-3 (1/час). Требуется вычислить вероятность безотказной работы передающей системы в течение времени t=100 (час), а также среднее время безотказной работы mtс, частоту отказов fc(t) и интенсивность отказов λс(t).
6. Определить количество резервных цепей в случае общего и раздельного «горячего» резервирования. Дано: Основная цепь содержит три последовательных элемента с вероятностью безотказной работы (в.б.р.) соответственно равной 0.8, 0.9, 0.7. Вероятность безотказной работы системы должна быть не менее 0.95. В.б.р. резервных элементов равна в.б.р. основным.
7. Покажите способы расчёта надёжности систем, представленных смешанным соединением элементов: мостиковая схема из пяти элементов. Представьте алгоритмы расчёта и формулы в общем виде.
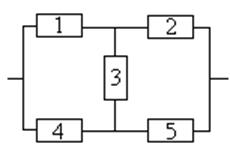
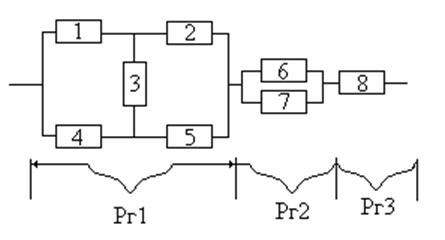

10. Привести расчёт надёжности в случае общего и раздельного «горячего» резерва в период нормальной эксплуатации (период «зрелости») для следующей структурной схемы:
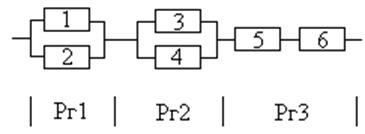
Расчёт выполнить для времени t=1000ч. Первая группа элементов (Рг1) элементы 1 и 2: Р1=0.95 и Р2=0.9. Элементы второй группы с независимой интенсивностью отказов имеют следующие вероятности безотказной работы: Р3=0.9, Р4=0.92. Третья группа элементов: Р5=0.95 и Р6=0.9. Рзад=0.95. Оценить также коэффициент повышения надёжности для обоих способов резервирования.
11. Привести расчёт надёжности в случае общего и раздельного «горячего» резерва в период нормальной эксплуатации (период «зрелости») для следующей структурной схемы:
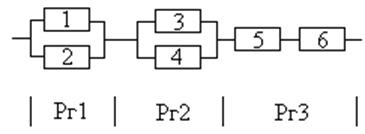
Расчёт выполнить для времени t=1000ч. Первая группа элементов (Рг1) элементы 1 и 2: Р1=0.95 и Р2=0.9. Элементы второй группы так же с независимой интенсивностью отказов имеют следующие вероятности безотказной работы (в.б.р.): Р3=0.9, Р4=0.92. Третья группа элементов: Р5=0.95 и Р6=0.9. Учесть при расчёте надёжности системы в.б.р. переключающего устройства (устройство, включающее резерв), равной 0.97 (Рпер=0.97). Рзад=0.95. Оценить также коэффициент повышения надёжности для обоих способов резервирования.
Выдал студентам 31.01.06
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.