Числовые характеристики системы двух случайных величин. Производящие функции. Распределение «xи квадрат». Распределение Стьюдента. Распределение Фишера

§18. Числовые характеристики системы

двух случайных величин.

Для описания системы двух случайных величин кроме математических ожиданий и дисперсий используют и другие характеристики. К их числу относятся ковариация и коэффициент коррекции.

o  Ковариацией между случайными величинами Х и Y называется число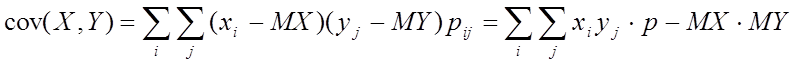, где .

Для непрерывных случайных величин X и Y используют формулу .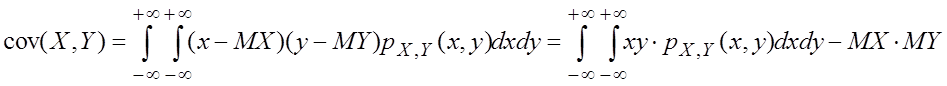

Покажем, что если случайные величины Х и Y независимы, то . Пусть Х и Y—непрерывные случайные величины

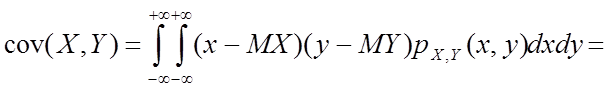
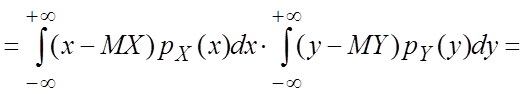
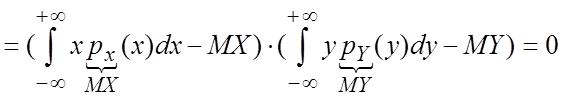
o  Коэффициентом корреляции между случайными величинами Х и Y называется число .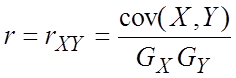

Свойства корреляции.

Свойство 1.  Абсолютная величина коэффициента корреляции не превосходит единицы, т.е. .

Свойство 2.  Для того чтобы  необходимо и достаточно, чтобы случайные величины Х и Y были связанны линейной зависимостью. Т.е. с вероятностью 1.

Свойство 3.  Если случайные величины независимы, то они некоррелированы, т.е. r=0.

Пусть Х и Y—независимы, тогда по свойству математического ожидания

o  Две случайные величины Х и Y называют коррелированными, если их коэффициент корреляции отличен от нуля.

o  Случайные величины Х и Y называют некоррелированными если их коэффициент корреляции равен 0.

Замечание. Из коррелированности двух случайных величин следует их зависимость, но из зависимости еще не вытекает коррелированность. Из независимости двух случайных величин следует их некоррелированность, но из некоррелированности еще нельзя заключить о независимости этих величин.

Коэффициент корреляции характеризует тенденцию случайных величин к линейной зависимости. Чем больше по абсолютной величине коэффициент корреляции, тем больше тенденция к линейной зависимости.

o  Коэффициентом асимметрии случайной величины Х называется число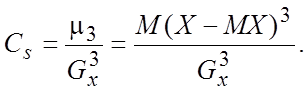

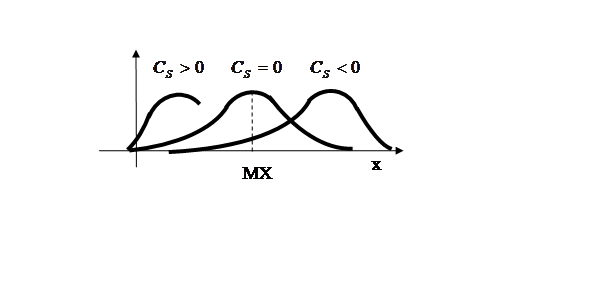
Знак коэффициента асимметрии указывает на правостороннюю или левостороннюю асимметрию.

o  Эксцессом случайной величины Х называется число .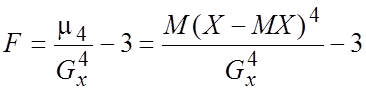

Характеризует сглаженность кривой распределения по отношению к кривой нормального распределения.

§ 19. Производящие функции.

o  Под целочисленной случайной величиной будем понимать дискретную случайную величину, которая может принимать значения 0,1,2,…

Таким образом, если случайная величина Х—целочисленная, то она имеет ряд распределения

Х	0	1	2	…
Р	р0	р1	р2	…

o  Пусть Х—целочисленная величина с законом распределения

Х	0	1	2	…
Р	р0	р1	р2	…

Ее производящей функцией называется функция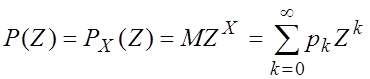

Свойства производящих функций.

Свойство 1.  Производящая функция  определена в области .

Свойство 2.  Производящая функция

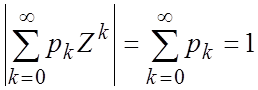
Свойство 3.  Значение производящей функции в точке Z=1,   P(1)=1. .

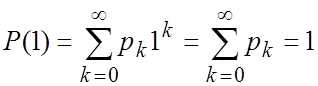Свойство 4.  Если Z=1, то MX=P’(1)

.

.

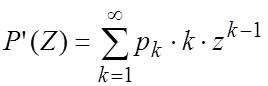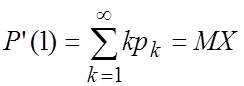Свойство 5. 

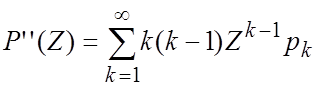. Если Z=1 .

.

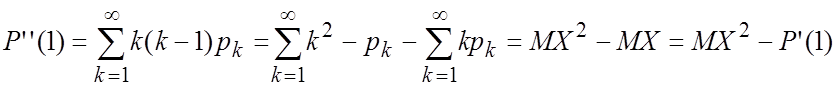Следовательно, .

Свойство 6.  Если Х₁,Х₂,…,Х_n—независимые целочисленные случайные величины, то производящая функция .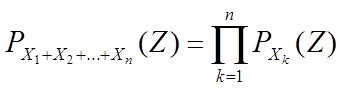

.

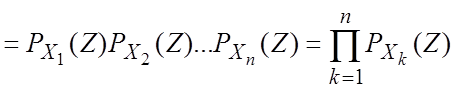Пример 1. Пусть μ—число успехов в n независимых испытаниях Бернулли, т.е. μ~B(n,p)—биномиальное распределение с параметрами (n,p). Найти производящую функцию случайной величины μ.

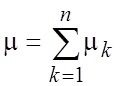, где μ_k—число успехов в каждом испытании

μk	0	1
P	q	p

Найдем производящую функцию случайной величины μ_k .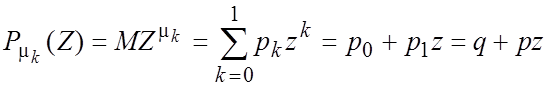

.

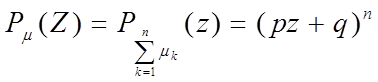Пример 2. Пусть случайная величина  имеет распределение Пуассона с параметром λ, т.е. . Найти производящую функцию случайной величины .

.

.

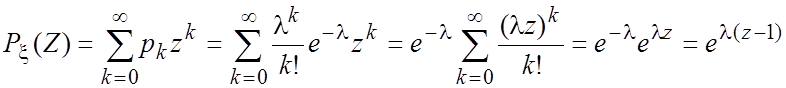§ 20. Распределение «xи квадрат».

Пусть X_i, —нормальные независимые случайные величины, причем математическое ожидании каждой из них равно нулю, а среднее квадратическое отклонение (или дисперсия)—единице. Тогда сумма квадратов этих величин 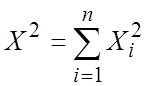 распределена по закону Х² с k=n степенями свободы. Если же эти величины Х_i связаны одним линейным соотношением, например 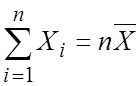, то число степеней свободы k=n-1.

Плотность этого распределения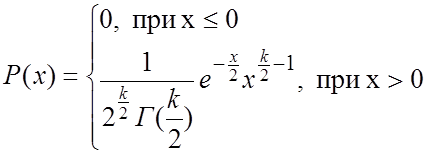, где 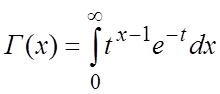—гамма-функция; в частности, Г(n+1)=n!

Отсюда видно, что распределение «x и квадрат» определяется одним параметром—числом степеней свободы k. С увеличением числа степеней свободы распределение медленно приближается к нормальному.

§ 21. Распределение Стьюдента.

Пусть Z—нормально распределенная величина, причем M(Z)=0, G²=1, т.е. Z~N(0,1), а V—независимая от Z величина, которая распределена по закону Х² с k степенями свободы. Тогда величина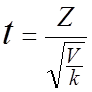 имеет распределение, которое называют t—распределением или распределением Стьюдента (псевдоним английского статистика В.Госсета), с k степенями свободы. С возрастанием числа степеней свободы распределение Стьюдента быстро приближается к нормальному.

Плотность распределения случайной величины t имеет вид ,  .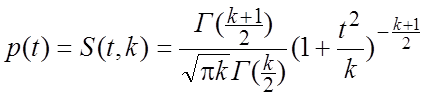

Случайная величина t имеет  математическое ожидание Mt=0, 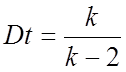 (k>2).

§ 22. Распределение Фишера.

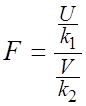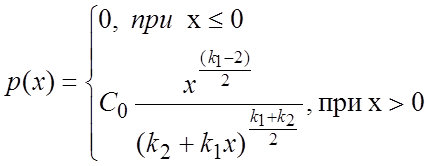Если U и V—независимые случайные величины, распределенные по закону Х² со степенями свободы k₁ и k₂, то величина  имеет распределение Фишера F со степенями свободы k₁ и k₂. Плотность этого распределения , где

.

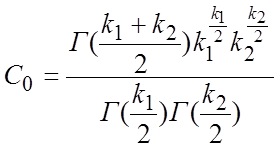Распределение Фишера F определяется двумя параметрами—числами степеней свободы.

§ 23. Характеристические функции.